2 3 N 6 3 4
News Co
May 02, 2025 · 6 min read
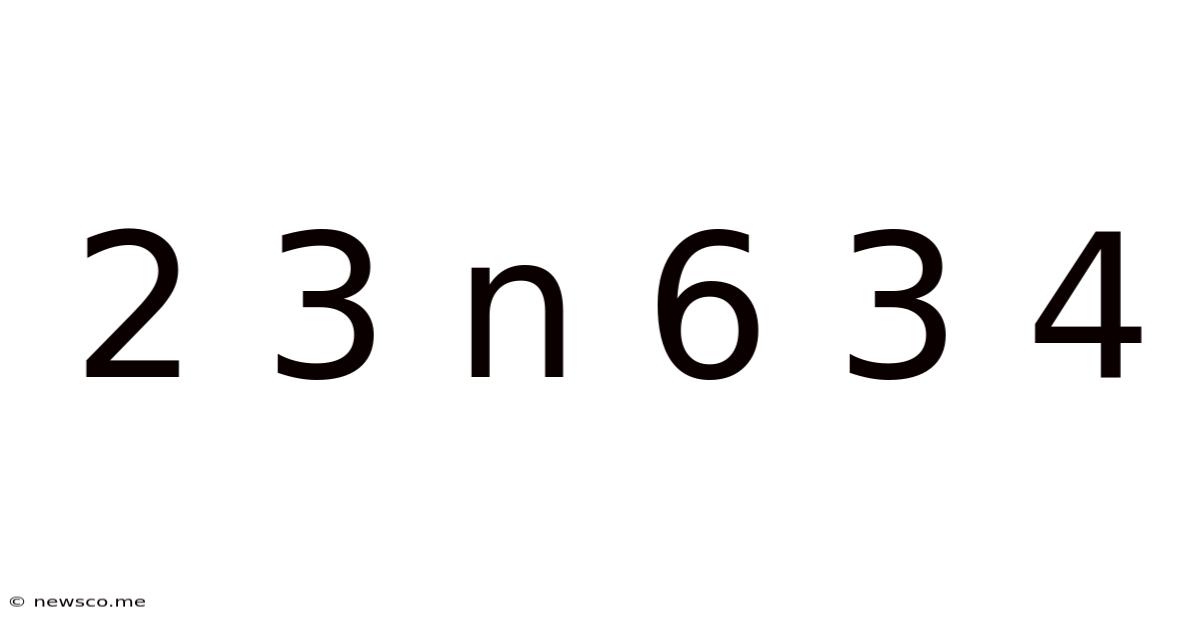
Table of Contents
Decoding the Sequence: 2 3 n 6 3 4 – A Deep Dive into Pattern Recognition and Mathematical Exploration
The seemingly simple sequence "2 3 n 6 3 4" presents a fascinating challenge. At first glance, it appears random. However, a deeper investigation reveals potential underlying patterns and mathematical relationships, sparking a journey into the world of pattern recognition, logical deduction, and creative problem-solving. This article will explore various approaches to understanding this sequence, highlighting the importance of critical thinking and the power of multiple perspectives in deciphering cryptic patterns.
Understanding the Problem: The Nature of Mathematical Sequences
Before delving into the specifics of "2 3 n 6 3 4," it's crucial to understand the general characteristics of mathematical sequences. Sequences are ordered lists of numbers, often following a specific rule or pattern. These patterns can be:
- Arithmetic: Each term is obtained by adding or subtracting a constant value to the previous term.
- Geometric: Each term is obtained by multiplying or dividing the previous term by a constant value.
- Fibonacci: Each term is the sum of the two preceding terms.
- Recursive: Each term is defined by a formula involving previous terms.
- Mixed: The sequence might incorporate elements of multiple types of sequences.
The challenge with "2 3 n 6 3 4" lies in identifying which type, if any, it follows or if it represents a more complex, possibly non-mathematical, pattern.
Approaches to Deciphering the Sequence: A Multi-pronged Strategy
Several approaches can be used to decipher the sequence "2 3 n 6 3 4," each offering a unique perspective:
1. The Brute-Force Approach: Searching for Simple Patterns
The most straightforward approach is to look for simple, readily apparent arithmetic or geometric progressions. However, this method quickly reveals its limitations with the given sequence. There's no immediately obvious constant difference or ratio between consecutive numbers. This lack of simple linearity suggests a more complex underlying structure.
2. The Analytical Approach: Seeking Mathematical Relationships
A more sophisticated approach involves exploring potential mathematical relationships between the numbers. We can consider:
- Differences between consecutive terms: Calculating the differences between consecutive terms can sometimes reveal patterns. While this doesn't immediately yield a clear pattern in our sequence, it doesn't rule out more complex relationships.
- Ratios between consecutive terms: Similar to differences, examining the ratios can reveal patterns. Again, a simple consistent ratio is not immediately apparent.
- Prime factorization: Breaking down the numbers into their prime factors (2 = 2, 3 = 3, 6 = 2 x 3, etc.) might reveal a hidden pattern based on prime distribution or relationships. This remains inconclusive with the present sequence, highlighting the need for further investigation.
3. The Combinatorial Approach: Exploring Permutations and Combinations
This approach considers the possibility that the sequence might represent a permutation or combination of a larger set of numbers. For example, are these numbers part of a larger sequence, a subset with a specific rule, or a re-arrangement based on some hidden criteria?
4. The Contextual Approach: Considering External Factors
A crucial step, often overlooked, involves examining potential external factors. The sequence could represent codes, date elements, coordinates, or other contextual information not explicitly given. Without additional context, this remains largely speculative but essential to keep in mind.
5. The Iterative Approach: Testing and Refining Hypotheses
Once initial patterns are identified (or not), an iterative approach is vital. This means continuously refining hypotheses based on the data and adjusting the approach as new information is discovered. This might involve exploring different mathematical operations, considering additional context, or even re-evaluating the initial assumptions about the nature of the sequence.
The Role of "n": The Wildcard
The inclusion of "n" introduces a significant level of uncertainty. It could represent:
- A variable: "n" might be a placeholder for a specific number governed by a rule that needs to be discovered.
- An unknown: It could simply indicate that one element in the sequence is missing or undefined.
- A symbolic representation: It might not represent a number at all but have a different symbolic meaning within a broader context.
Potential Interpretations and Solutions (Speculative)
Given the inherent ambiguities, several speculative interpretations are possible. Without a clear context or additional information, definitive solutions are unlikely. These interpretations illustrate the creative problem-solving needed in deciphering cryptic sequences.
Interpretation 1: A Recursive Sequence with a Hidden Rule
It's possible the sequence follows a recursive rule where the value of "n" depends on preceding or subsequent numbers. The rule might be complex, involving multiple operations or even non-linear relationships. Discovering this rule requires extensive testing and hypothesis refinement.
Interpretation 2: A Modular Arithmetic Sequence
The numbers could represent residues (remainders) after division by a specific number. Exploring modular arithmetic might reveal hidden relationships, but this requires careful analysis and the consideration of different moduli.
Interpretation 3: A Coded Message or Representation
The sequence could be a code representing letters, symbols, or other information. The number "n" might be a crucial element of the code, possibly acting as a delimiter or a key to decipher the message. This interpretation requires a deeper understanding of potential coding schemes.
Interpretation 4: A Pattern Based on Differences or Ratios
While simple differences and ratios don't immediately yield an obvious pattern, examining second-order differences (differences between the differences) or ratios of ratios could potentially reveal a more subtle mathematical relationship. This is a more complex analytical approach.
The Importance of Context and Further Investigation
The key takeaway is the significance of context. Without additional information or constraints, the sequence "2 3 n 6 3 4" remains open to multiple interpretations. Its solution requires a flexible approach involving pattern recognition, mathematical exploration, creative problem-solving, and the iterative testing and refinement of hypotheses.
Further investigation might involve:
- Additional data points: If more numbers were added to the sequence, identifying a clear pattern might become easier.
- Clarification on "n": Understanding the meaning and role of "n" is vital to unlock the sequence's underlying structure.
- External context: Knowing the origin or purpose of the sequence could significantly narrow down the possibilities.
Conclusion: Embracing the Challenge of Pattern Recognition
The sequence "2 3 n 6 3 4" serves as a compelling illustration of the challenges and rewards of pattern recognition. It underscores the need for multiple approaches, critical thinking, creative problem-solving, and the iterative process of hypothesis testing and refinement. While a definitive solution remains elusive without additional information, the journey of exploration itself is a testament to the power of mathematical thinking and the beauty of hidden patterns. The ambiguity itself is a prompt for further exploration and a reminder that not all puzzles have readily apparent solutions.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 3 N 6 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.