2/3 Of A Cup Times 3
News Co
Apr 19, 2025 · 5 min read
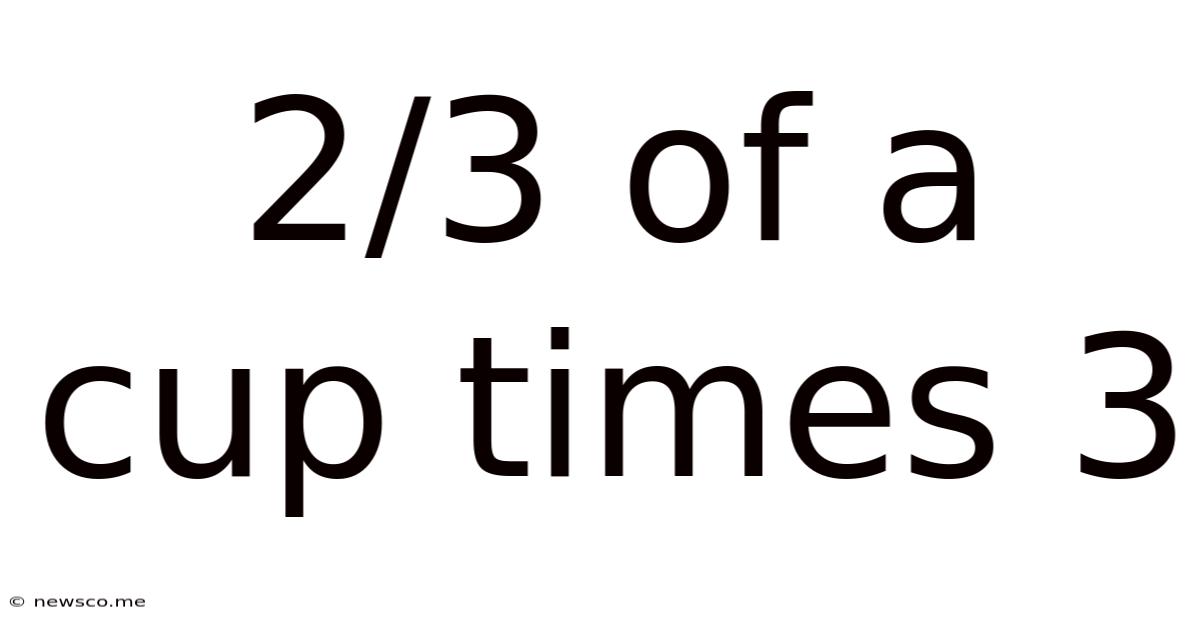
Table of Contents
2/3 of a Cup Times 3: A Deep Dive into Fractions, Measurement, and Baking Precision
This seemingly simple question – "what is 2/3 of a cup times 3?" – opens a door to a fascinating world of fractions, accurate measurement, and the importance of precision, especially in cooking and baking. While the answer itself is straightforward, understanding the underlying mathematical principles and practical applications makes this a topic worth exploring in detail. This article will delve into the calculation, explore its significance in various contexts, and offer valuable tips for working with fractions in everyday life.
Understanding the Basics: Fractions and Multiplication
Before tackling the specific problem, let's refresh our understanding of fractions and how they interact with multiplication. A fraction represents a part of a whole. In the expression "2/3," the "2" is the numerator (the number of parts we have) and the "3" is the denominator (the total number of equal parts the whole is divided into).
Multiplying fractions involves multiplying the numerators together and the denominators together. For example:
(a/b) * (c/d) = (a * c) / (b * d)
In our case, we're multiplying 2/3 by 3, which can be written as 3/1 (any whole number can be expressed as a fraction with a denominator of 1). Therefore, the calculation becomes:
(2/3) * (3/1) = (2 * 3) / (3 * 1) = 6/3
Simplifying the fraction 6/3, we get 2. Therefore, 2/3 of a cup times 3 equals 2 cups.
The Practical Implications: Cooking and Baking
The ability to accurately perform these calculations is crucial in cooking and baking. Recipes often call for fractional amounts of ingredients, and understanding how to adjust these amounts based on the number of servings is essential for achieving consistent results. Incorrect measurements can drastically alter the texture, taste, and overall quality of a dish.
Imagine you're making a cake recipe that calls for 2/3 cup of sugar. If you want to double the recipe, you need to multiply the amount of sugar by 2. This requires understanding that 2/3 * 2 = 4/3, which simplifies to 1 and 1/3 cups of sugar. Similarly, if you want to triple the recipe, you use the calculation we just performed – resulting in 2 cups of sugar.
Beyond the Simple Calculation: Adapting Recipes
The calculation of "2/3 of a cup times 3" extends beyond a simple mathematical exercise. It represents the core of scaling recipes. Many bakers and cooks utilize this principle to adjust recipes to suit different needs. Whether it's making enough cookies for a party, adapting a recipe to serve a smaller number of people, or scaling recipes up for large-scale catering, the ability to manipulate fractional quantities with precision is vital. In these scenarios, it's important to consider the behaviour of different ingredients when scaling up or down a recipe. Certain ingredients, like liquids, may be more forgiving of scaling than others, while others might require a slight adjustment to maintain desired consistency.
For example:
- Scaling down: If a recipe calls for 1 ½ cups of flour and you want to make half the recipe, you calculate 1 ½ / 2 = ¾ cups of flour.
- Scaling up: If a recipe calls for ⅓ cup of butter and you're tripling the recipe, you'd calculate ⅓ * 3 = 1 cup of butter.
Mastering these fractional calculations improves your baking prowess, helping create delectable recipes flawlessly.
Beyond Baking: Applications in Other Fields
The principles of multiplying fractions aren't limited to the culinary arts. Understanding these concepts has wide-ranging applications across numerous fields:
- Construction and Engineering: Precise measurements are paramount in construction and engineering. Calculating material quantities, determining distances, and ensuring structural integrity often involve complex fractional calculations.
- Science and Research: In scientific experiments and research, accurate measurements and calculations are crucial for reliable results. Fractions are used extensively in data analysis and calculations.
- Finance and Economics: Fractions are used in calculating interest rates, shares, and other financial metrics.
- Everyday Life: Dividing items, sharing resources, and measuring ingredients in everyday situations often require basic fraction manipulation.
Mastering Fraction Multiplication: Tips and Tricks
For those who find working with fractions challenging, here are some helpful tips and tricks:
- Visual Aids: Using visual aids like pie charts or fraction circles can make it easier to grasp the concept of fractions and their multiplication.
- Practice Regularly: Regular practice is key to mastering any mathematical concept. Start with simple problems and gradually move towards more complex ones.
- Online Resources: Numerous online resources, including videos and interactive tutorials, offer help in understanding fractions.
- Convert to Decimals: Sometimes converting fractions to decimals can simplify the calculation process, especially for more complex problems. For instance, 2/3 is approximately 0.667. Therefore, 0.667 x 3 ≈ 2. This approximation is useful in many situations but lacks the precision of working with fractions directly.
- Simplify Before Multiplying: Simplifying fractions before multiplying can make the calculation easier. For example, in (2/3) * (3/1), you can cancel out the common factor "3" before multiplying, making the calculation simpler.
Conclusion: The Importance of Precision
The seemingly simple question of "2/3 of a cup times 3" highlights the importance of understanding fractions and their practical applications. From the precision needed in baking to the accuracy required in various scientific fields, mastering fractional calculations is a valuable skill. By understanding the underlying principles and utilizing helpful tips and tricks, anyone can confidently work with fractions and achieve accurate results in a variety of contexts. The ability to perform these calculations confidently contributes to success, not only in the kitchen but also in various aspects of life where precise measurements and calculations are necessary. So, next time you're faced with a fractional calculation, remember the journey from 2/3 of a cup times 3 to a full understanding of its wider implications. This journey emphasizes the importance of numerical literacy and its profound impact on our ability to navigate the world around us effectively. The journey, from the initial calculation to understanding its wider applications, proves to be a rewarding experience in mathematical understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2/3 Of A Cup Times 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.