2/3 X 2/3 X 2/3 X 2/3
News Co
Apr 13, 2025 · 5 min read
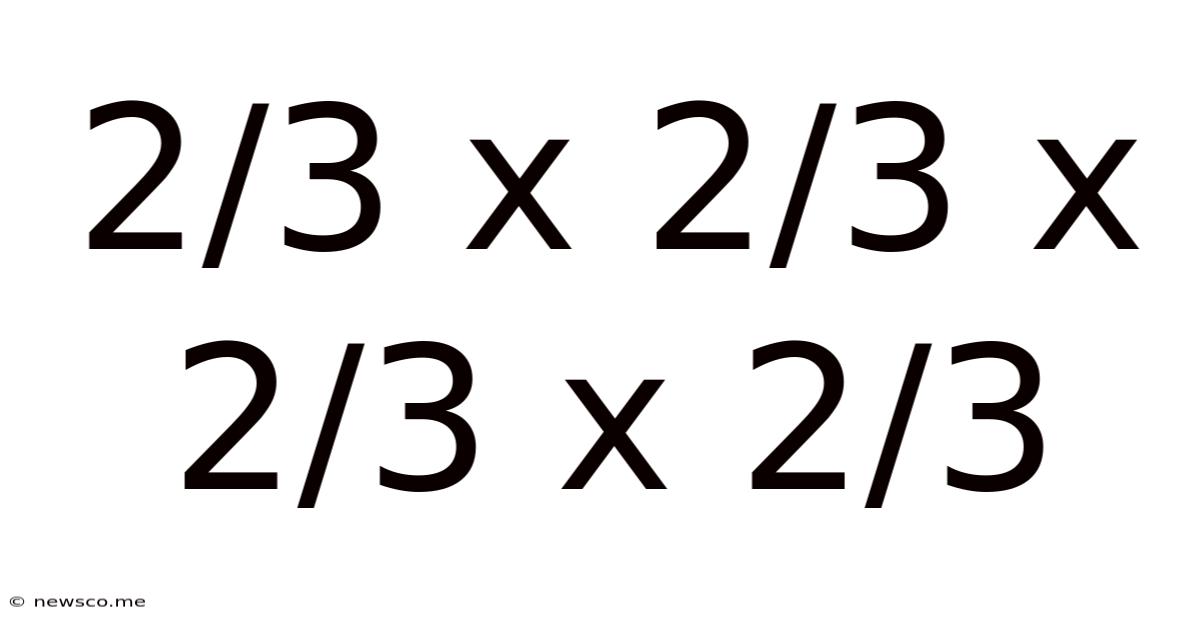
Table of Contents
Decoding the Mystery of 2/3 x 2/3 x 2/3 x 2/3: A Deep Dive into Repeated Multiplication
The seemingly simple mathematical expression, 2/3 x 2/3 x 2/3 x 2/3, presents a fascinating opportunity to explore several key mathematical concepts. While the calculation itself is straightforward, understanding the underlying principles and their broader applications unveils a wealth of knowledge relevant to various fields, from basic arithmetic to advanced calculus. This article will not only solve the equation but also delve into the intricacies of repeated multiplication, its representation in different forms, and its practical uses.
Understanding Repeated Multiplication: Beyond Basic Arithmetic
At its core, the expression 2/3 x 2/3 x 2/3 x 2/3 represents repeated multiplication, a fundamental concept in mathematics. Repeated multiplication, also known as exponentiation, involves multiplying a number by itself a specified number of times. This is often expressed using exponents. In our case, we can rewrite the expression using exponential notation: (2/3)⁴. Here, 2/3 is the base, and 4 is the exponent, indicating that 2/3 is multiplied by itself four times.
The Power of Exponents: Simplifying Complex Calculations
The use of exponents significantly simplifies complex calculations involving repeated multiplication. Instead of writing out a long string of multiplications, we can concisely represent the operation using a base and an exponent. This not only saves time and space but also improves the clarity and readability of mathematical expressions. Imagine trying to work with (2/3)^10 or even larger exponents; the exponential notation becomes indispensable.
Exploring the Properties of Exponents
Understanding the properties of exponents is crucial for manipulating and solving equations involving repeated multiplication. These properties include:
- Product of Powers: When multiplying two numbers with the same base, you add the exponents: aᵐ x aⁿ = aᵐ⁺ⁿ
- Quotient of Powers: When dividing two numbers with the same base, you subtract the exponents: aᵐ ÷ aⁿ = aᵐ⁻ⁿ
- Power of a Power: When raising a power to another power, you multiply the exponents: (aᵐ)ⁿ = aᵐⁿ
- Power of a Product: When raising a product to a power, you raise each factor to that power: (ab)ⁿ = aⁿbⁿ
- Power of a Quotient: When raising a quotient to a power, you raise both the numerator and the denominator to that power: (a/b)ⁿ = aⁿ/bⁿ
These properties are essential tools for simplifying complex expressions and solving equations involving exponents. We'll use these properties later to explore variations and extensions of our initial problem.
Solving 2/3 x 2/3 x 2/3 x 2/3: A Step-by-Step Approach
Now, let's solve the equation 2/3 x 2/3 x 2/3 x 2/3, or (2/3)⁴. We can approach this in a few ways:
Method 1: Direct Multiplication
This is the most straightforward method. We simply multiply the fractions sequentially:
2/3 x 2/3 = 4/9 4/9 x 2/3 = 8/27 8/27 x 2/3 = 16/81
Therefore, 2/3 x 2/3 x 2/3 x 2/3 = 16/81.
Method 2: Using Exponential Properties
As mentioned earlier, we can rewrite the expression as (2/3)⁴. Using the power of a quotient property, we can raise both the numerator and the denominator to the power of 4:
(2/3)⁴ = 2⁴/3⁴ = 16/81
This method provides a more concise and efficient solution, especially when dealing with larger exponents.
Extending the Concept: Exploring Variations and Applications
The basic calculation (2/3)⁴ provides a foundation for exploring more complex scenarios and real-world applications. Consider these variations:
Scenario 1: Repeated Multiplication with Different Bases
What if we had an expression like (2/3)⁴ x (1/2)³? We would apply the same principles of exponents, calculating each term separately and then multiplying the results. This introduces the concept of mixed bases and requires a solid understanding of order of operations (PEMDAS/BODMAS).
Scenario 2: Solving for the Exponent
Instead of knowing the exponent and calculating the result, we might be asked to find the exponent that results in a specific value. For example: (2/3)ˣ = 16/81. In this case, we'd use logarithmic functions to solve for 'x', which is 4.
Scenario 3: Real-World Applications
Repeated multiplication finds practical use in numerous fields:
- Compound Interest: Calculating compound interest involves repeated multiplication. The principal amount is repeatedly multiplied by the interest rate over a certain period.
- Population Growth: Modeling population growth often uses exponential functions, where the initial population is repeatedly multiplied by a growth factor.
- Radioactive Decay: The decay of radioactive materials follows an exponential decay model, where the initial amount is repeatedly multiplied by a decay factor.
- Probability: In probability, repeated independent events are often modeled using repeated multiplication of probabilities.
Conclusion: Beyond the Calculation
The seemingly simple calculation 2/3 x 2/3 x 2/3 x 2/3 provides a springboard for exploring a wide range of mathematical concepts and their practical applications. By understanding repeated multiplication, exponential notation, and the properties of exponents, we can tackle more complex problems and appreciate the power and versatility of these fundamental tools. The value of this exercise lies not just in obtaining the answer (16/81) but in comprehending the underlying principles and their significance across diverse fields. This deeper understanding will enhance your mathematical skills and broaden your ability to solve real-world problems. Further exploration into these concepts will open doors to even more advanced mathematical topics and applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2/3 X 2/3 X 2/3 X 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.