2 4 8 16 32 64
News Co
May 02, 2025 · 5 min read
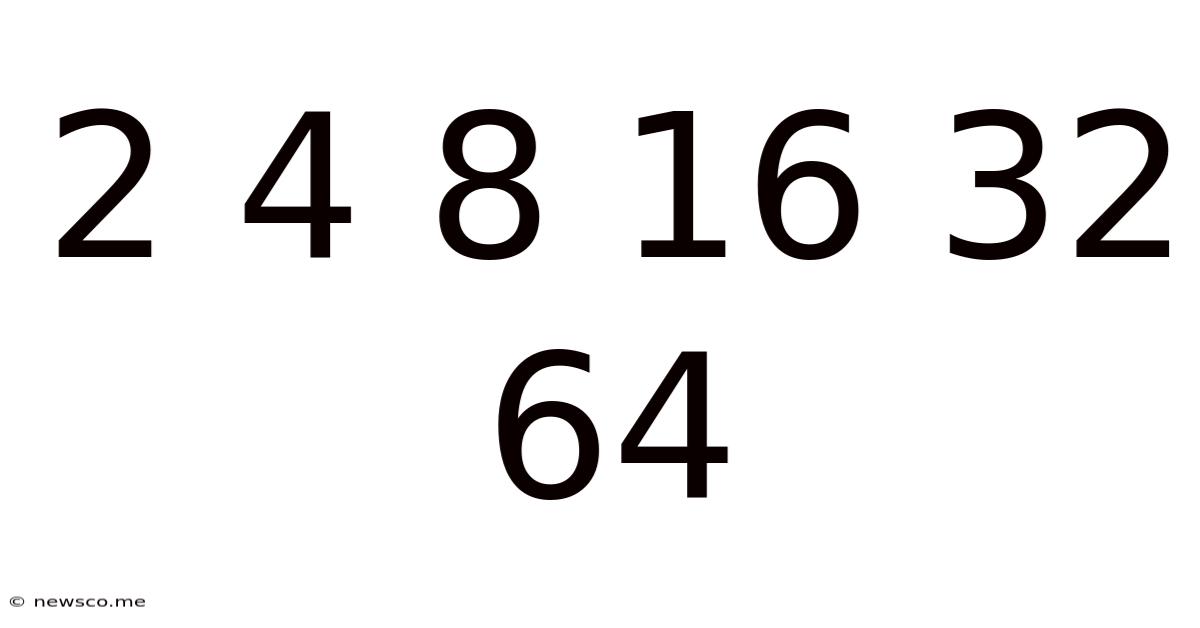
Table of Contents
Decoding the Power of 2, 4, 8, 16, 32, 64: A Deep Dive into Exponential Growth and its Applications
The seemingly simple sequence 2, 4, 8, 16, 32, 64... holds a profound significance across diverse fields, from mathematics and computer science to finance and even nature itself. This isn't just a random progression; it represents the power of exponential growth, a concept that shapes our understanding of everything from compound interest to the spread of information in the digital age. This article delves deep into this fascinating sequence, exploring its mathematical underpinnings, its applications in various disciplines, and the broader implications of exponential growth in our world.
The Mathematical Heart of the Sequence: Geometric Progression
At its core, the sequence 2, 4, 8, 16, 32, 64 is a geometric progression. A geometric progression is a sequence where each term is found by multiplying the previous term by a constant value, known as the common ratio. In this specific sequence, the common ratio is 2. Each number is double the preceding one:
- 2 x 2 = 4
- 4 x 2 = 8
- 8 x 2 = 16
- 16 x 2 = 32
- 32 x 2 = 64
This simple multiplication process leads to remarkably rapid growth. This rapid increase is a hallmark of exponential growth, a pattern that contrasts sharply with linear growth, where the increase is constant.
Understanding Exponential Growth vs. Linear Growth
To fully grasp the impact of this sequence, let's compare exponential growth to linear growth. Imagine two scenarios:
-
Scenario 1 (Linear Growth): You earn $10 per day. After 6 days, you'll have $60. The growth is consistent.
-
Scenario 2 (Exponential Growth): You start with $1 and double your money each day. After 6 days, you'll have $64. The growth accelerates dramatically.
This difference becomes even more striking over longer periods. While linear growth increases at a constant rate, exponential growth increases at an increasing rate. This is the key characteristic that makes exponential sequences like 2, 4, 8, 16, 32, 64 so powerful and, in some cases, potentially overwhelming.
Applications Across Diverse Fields
The principles behind the sequence 2, 4, 8, 16, 32, 64 manifest in numerous real-world applications:
1. Computer Science and Binary Systems
The sequence is fundamental to computer science because it directly reflects the binary number system. Computers operate using bits, which represent either 0 or 1. The powers of 2 (2, 4, 8, 16, 32, 64, etc.) determine the number of possible states a given number of bits can represent. For example:
- 1 bit: 2 states (0 or 1)
- 2 bits: 4 states (00, 01, 10, 11)
- 3 bits: 8 states (000, 001, 010, 011, 100, 101, 110, 111)
This directly impacts memory capacity, data transfer rates, and various other aspects of computer architecture. Understanding powers of 2 is crucial for any computer scientist or programmer.
2. Finance and Compound Interest
In finance, exponential growth is synonymous with compound interest. When interest is compounded, it's calculated not only on the principal amount but also on the accumulated interest from previous periods. This creates a snowball effect, leading to exponential growth of the investment over time. The faster the compounding frequency (daily, monthly, annually), the more pronounced the exponential effect becomes.
3. Biology and Population Growth
Exponential growth models are often used in biology to describe the growth of populations under ideal conditions – abundant resources, no predators, and no disease. While this type of unrestricted growth is rarely sustained in the long term, it provides a valuable initial model for understanding population dynamics.
4. Networking and Data Transmission
In networking, the sequence 2, 4, 8, 16, 32, 64 appears in various contexts. For example, IP addresses are often represented using binary notation, and network topologies can sometimes exhibit patterns related to powers of 2. Data transmission speeds and bandwidth capacities frequently involve multiples of 2 as well.
5. Music and Musical Scales
Interestingly, the sequence also finds its way into music theory. Many musical scales and intervals are based on ratios that involve powers of 2, leading to harmonic relationships that are pleasing to the ear. The octave, for instance, represents a doubling of frequency, directly relating to the sequence.
The Implications of Exponential Growth: A Double-Edged Sword
While the power of exponential growth is undeniable and beneficial in many contexts (e.g., financial investments), it also carries significant implications, especially when considering potential downsides:
-
Rapid Resource Depletion: Exponential population growth or resource consumption can quickly outpace the Earth's capacity to sustain them, leading to environmental challenges.
-
Uncontrolled Spread of Information: The rapid spread of information, both true and false, via social media and the internet exemplifies exponential growth. This can result in misinformation campaigns and the rapid escalation of crises.
-
Technological Advancements: Moore's Law, which states that the number of transistors on a microchip doubles approximately every two years, is a prime example of exponential technological advancement. While this has led to incredible progress, it also raises concerns about potential disruptions and unforeseen consequences.
-
Financial Bubbles: Speculative bubbles in financial markets can exhibit exponential growth until they inevitably burst, leading to significant economic downturns.
Conclusion: Embracing the Power, Mitigating the Risks
The sequence 2, 4, 8, 16, 32, 64 is more than just a simple mathematical progression. It embodies the essence of exponential growth, a force that shapes our world in profound ways. Understanding its underlying principles is critical for navigating the complexities of our increasingly interconnected and rapidly changing world. While harnessing the power of exponential growth can lead to remarkable advancements in various fields, it's crucial to acknowledge and mitigate the potential risks associated with its unchecked expansion. This requires a balanced approach that leverages the benefits of exponential progress while proactively addressing the potential challenges it presents. By understanding both the opportunities and the limitations, we can better prepare ourselves for the future shaped by this fundamental mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 4 8 16 32 64 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.