2/5 + 1/3 Simplified As A Fraction
News Co
May 07, 2025 · 5 min read
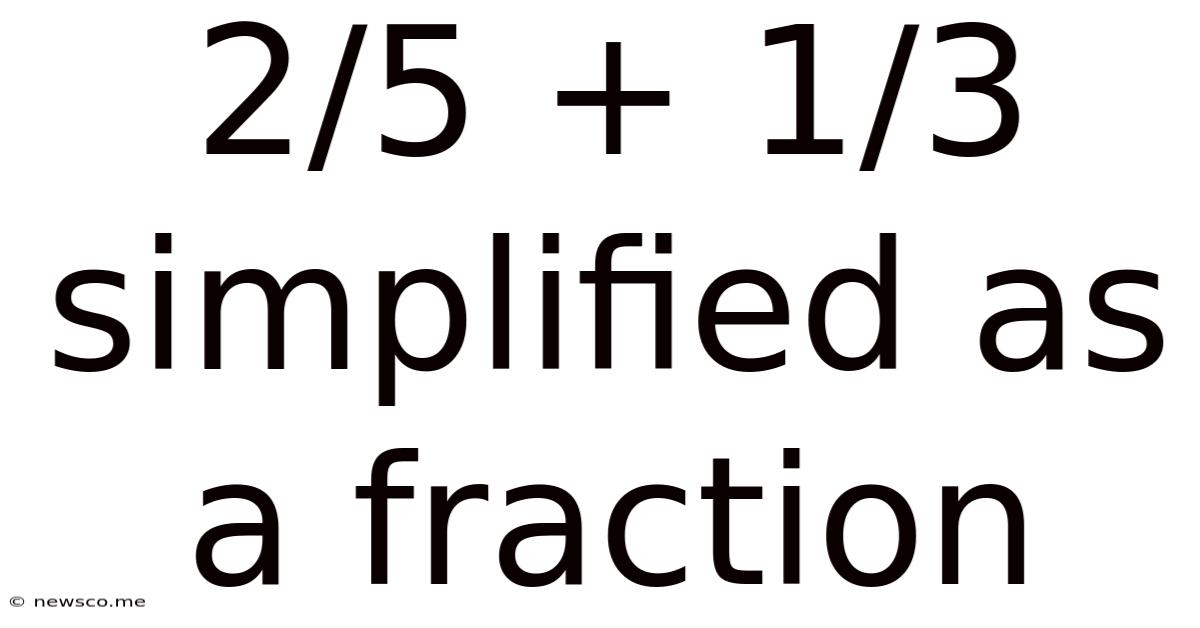
Table of Contents
Simplifying Fractions: A Deep Dive into 2/5 + 1/3
Adding fractions might seem like a simple arithmetic task, but understanding the underlying principles and mastering the techniques is crucial for various mathematical applications. This comprehensive guide delves into the process of simplifying the fraction 2/5 + 1/3, explaining each step in detail and exploring related concepts to enhance your understanding of fraction arithmetic. We'll cover not just the solution, but also the broader context of fraction addition and simplification.
Understanding Fractions: A Quick Recap
Before we tackle the addition problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number represents the number of parts we have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For example, in the fraction 2/5, the numerator is 2 (we have 2 parts), and the denominator is 5 (the whole is divided into 5 equal parts).
Adding Fractions with Different Denominators
The key to adding fractions like 2/5 and 1/3 lies in understanding that we can only directly add fractions when they share the same denominator (a common denominator). Since 2/5 and 1/3 have different denominators, we need to find a common denominator before we can add them.
Finding the Least Common Denominator (LCD)
The least common denominator (LCD) is the smallest number that is a multiple of both denominators. There are several ways to find the LCD:
-
Listing Multiples: List the multiples of each denominator until you find a common multiple. Multiples of 5 are 5, 10, 15, 20, 25... Multiples of 3 are 3, 6, 9, 12, 15... The smallest common multiple is 15.
-
Prime Factorization: Break down each denominator into its prime factors. 5 is a prime number, and 3 is a prime number. The LCD is the product of the highest powers of all prime factors present in either denominator. In this case, LCD = 5 x 3 = 15.
-
Using the Formula (if applicable): If the denominators are relatively prime (they share no common factors other than 1), the LCD is simply the product of the two denominators. This applies in our case, as 5 and 3 are relatively prime.
Converting Fractions to Equivalent Fractions
Once we've found the LCD (which is 15), we need to convert each fraction into an equivalent fraction with a denominator of 15. To do this, we multiply both the numerator and the denominator of each fraction by the same number that makes the denominator equal to 15.
-
For 2/5: To change the denominator from 5 to 15, we multiply by 3 (because 5 x 3 = 15). Therefore, we multiply both the numerator and the denominator by 3: (2 x 3) / (5 x 3) = 6/15
-
For 1/3: To change the denominator from 3 to 15, we multiply by 5 (because 3 x 5 = 15). Therefore, we multiply both the numerator and the denominator by 5: (1 x 5) / (3 x 5) = 5/15
Adding the Fractions
Now that both fractions have the same denominator (15), we can add them simply by adding their numerators and keeping the denominator the same:
6/15 + 5/15 = (6 + 5) / 15 = 11/15
Simplifying the Resulting Fraction
The fraction 11/15 is already in its simplest form. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and the denominator is 1. In this case, the GCD of 11 and 15 is 1, meaning the fraction cannot be simplified further.
Real-World Applications of Fraction Addition
Adding fractions isn't just an abstract mathematical exercise; it has numerous real-world applications:
-
Baking and Cooking: Recipes often require fractional measurements of ingredients. Adding fractions helps in calculating the total amount of an ingredient needed.
-
Construction and Engineering: Precise measurements are essential in construction and engineering, and fractions are frequently used to represent dimensions and quantities.
-
Finance: Working with budgets and financial statements involves dealing with fractions and percentages, requiring addition and other fraction operations.
-
Data Analysis: In statistics and data analysis, fractions and proportions are used extensively to represent data and relationships, necessitating fraction arithmetic.
Advanced Concepts Related to Fraction Arithmetic
Let's explore some more advanced concepts related to fractions, building upon our understanding of fraction addition:
Subtracting Fractions:
Subtracting fractions follows a similar process to addition. Find the LCD, convert to equivalent fractions, and then subtract the numerators while keeping the denominator the same.
Multiplying Fractions:
Multiplying fractions is simpler than adding or subtracting. Multiply the numerators together and multiply the denominators together. Simplify the resulting fraction if possible.
Dividing Fractions:
To divide fractions, invert (flip) the second fraction (the divisor) and then multiply the fractions.
Mixed Numbers:
A mixed number consists of a whole number and a fraction (e.g., 1 1/2). To add, subtract, multiply, or divide mixed numbers, it's usually best to convert them into improper fractions first (where the numerator is greater than or equal to the denominator). An improper fraction equivalent to 1 1/2 would be 3/2.
Troubleshooting Common Mistakes in Fraction Arithmetic
Several common mistakes can occur when working with fractions:
-
Forgetting to find the LCD: Attempting to add fractions with different denominators directly leads to incorrect results.
-
Incorrectly converting fractions: Errors in multiplying the numerator and denominator by the same factor can lead to inaccurate equivalent fractions.
-
Not simplifying the result: Leaving the answer as an unsimplified fraction is considered incomplete.
-
Misunderstanding mixed numbers: Incorrectly converting mixed numbers to improper fractions or vice-versa can cause errors in calculations.
Conclusion: Mastering Fraction Arithmetic for Success
Adding fractions, like simplifying 2/5 + 1/3 to 11/15, is a fundamental skill with wide-ranging applications. By understanding the underlying principles, mastering the techniques of finding the LCD, converting to equivalent fractions, and simplifying the result, you can confidently tackle more complex fraction problems and apply this crucial skill to various real-world scenarios. Remember to practice regularly and review the concepts to solidify your understanding and avoid common pitfalls. Proficiency in fraction arithmetic is a cornerstone of mathematical literacy and opens doors to advanced mathematical studies and real-world problem-solving.
Latest Posts
Latest Posts
-
4 Sides And 4 Right Angles
May 08, 2025
-
1 To 2000 Copy And Paste
May 08, 2025
-
How Many Terms In A Polynomial
May 08, 2025
-
Are Multiples Of 4 Always Even
May 08, 2025
-
How To Find Angles In A Quadrilateral
May 08, 2025
Related Post
Thank you for visiting our website which covers about 2/5 + 1/3 Simplified As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.