2/5 As A Decimal And Percentage
News Co
Apr 15, 2025 · 5 min read
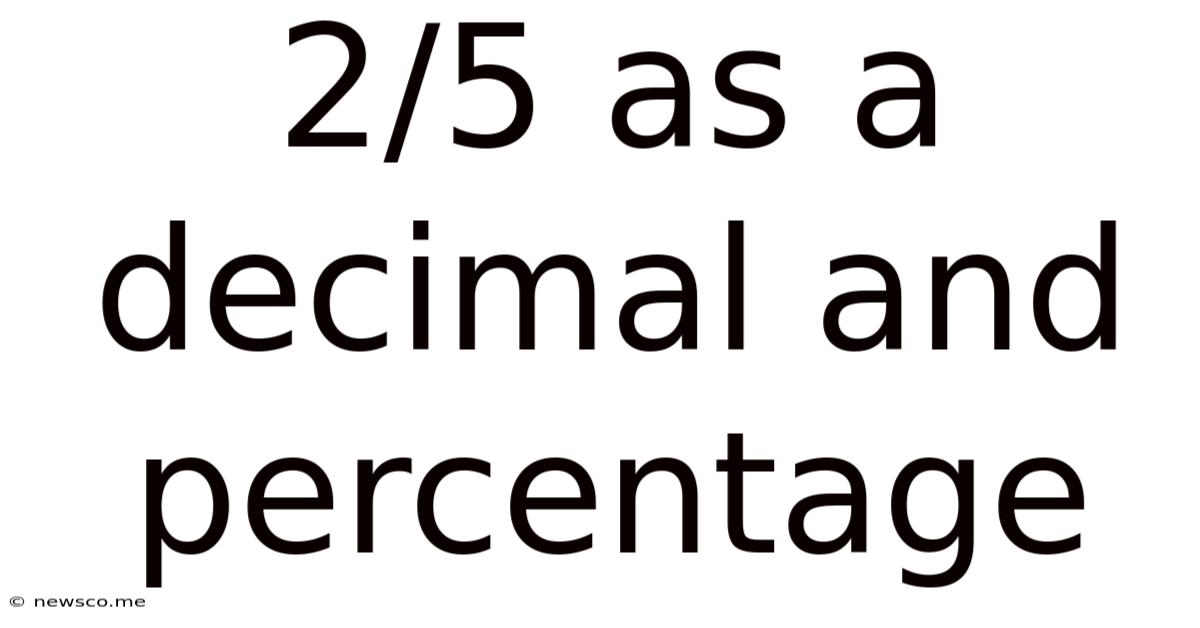
Table of Contents
2/5 as a Decimal and Percentage: A Comprehensive Guide
Understanding fractions, decimals, and percentages is fundamental to various aspects of life, from everyday finances to complex scientific calculations. This comprehensive guide delves into the conversion of the fraction 2/5 into its decimal and percentage equivalents, explaining the process in detail and exploring related concepts. We'll also examine various applications and provide practical examples to solidify your understanding.
Understanding Fractions, Decimals, and Percentages
Before we dive into the conversion of 2/5, let's refresh our understanding of these three interconnected numerical representations:
Fractions: Fractions represent a part of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator shows the total number of equal parts the whole is divided into. For example, in the fraction 2/5, 2 is the numerator and 5 is the denominator. This means we have 2 parts out of a total of 5 equal parts.
Decimals: Decimals are another way of expressing parts of a whole. They use a base-ten system, with a decimal point separating the whole number from the fractional part. Each position to the right of the decimal point represents a decreasing power of ten (tenths, hundredths, thousandths, and so on). For instance, 0.5 represents five-tenths (5/10).
Percentages: Percentages represent a fraction or decimal as a portion of 100. The percentage symbol (%) indicates "per hundred." For example, 50% means 50 out of 100, which is equivalent to 50/100 or 0.5.
Converting 2/5 to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. In the case of 2/5:
1. Perform the Division: Divide 2 by 5: 2 ÷ 5 = 0.4
Therefore, 2/5 as a decimal is 0.4.
Converting 2/5 to a Percentage
There are two primary methods for converting 2/5 to a percentage:
Method 1: Using the Decimal Equivalent
Since we already know that 2/5 is equal to 0.4, we can convert this decimal to a percentage by multiplying it by 100 and adding the percentage symbol:
0.4 x 100 = 40
Therefore, 2/5 as a percentage is 40%.
Method 2: Direct Conversion from Fraction
We can also convert 2/5 to a percentage directly by finding an equivalent fraction with a denominator of 100:
To do this, we need to determine what number multiplied by 5 equals 100. This is 20 (100 ÷ 5 = 20). We then multiply both the numerator and the denominator of 2/5 by 20:
(2 x 20) / (5 x 20) = 40/100
Since 40/100 represents 40 out of 100, this is equivalent to 40%.
Real-World Applications of 2/5, 0.4, and 40%
The understanding and application of these equivalent representations are crucial in many real-world scenarios:
- Sales and Discounts: A 40% discount on an item means you pay only 60% of the original price.
- Financial Calculations: Interest rates, loan repayments, and investment returns are often expressed as percentages.
- Statistics and Data Analysis: Percentages are widely used to represent proportions and probabilities in statistical analysis.
- Measurement and Conversion: Understanding decimals is essential for precise measurements in various fields like engineering and science.
- Everyday Life: From calculating tips in restaurants to understanding the proportion of ingredients in a recipe, these concepts are invaluable in our daily lives.
Further Exploration: Working with Other Fractions
The methods used to convert 2/5 to a decimal and percentage can be applied to other fractions as well. Here's a breakdown of the process, along with some examples:
Converting Fractions to Decimals:
- Divide the numerator by the denominator. This yields the decimal equivalent.
Examples:
- 3/4 = 3 ÷ 4 = 0.75
- 1/8 = 1 ÷ 8 = 0.125
- 7/10 = 7 ÷ 10 = 0.7
- 5/6 = 5 ÷ 6 = 0.8333... (this is a repeating decimal)
Converting Fractions to Percentages:
- Convert the fraction to a decimal (as shown above).
- Multiply the decimal by 100 and add the percentage symbol (%).
Examples:
- 3/4 = 0.75 x 100 = 75%
- 1/8 = 0.125 x 100 = 12.5%
- 7/10 = 0.7 x 100 = 70%
- 5/6 = 0.8333... x 100 ≈ 83.33% (Note: we often round repeating decimals)
Alternatively, you can find an equivalent fraction with a denominator of 100:
- Determine the factor needed to multiply the denominator to reach 100.
- Multiply both the numerator and denominator by this factor.
- The numerator of the new fraction represents the percentage.
Examples:
- 3/4: To get from 4 to 100, multiply by 25. (3 x 25)/(4 x 25) = 75/100 = 75%
- 1/8: To get from 8 to 100, we can't find a whole number factor, making the decimal method more efficient in this case.
Dealing with Repeating Decimals
Some fractions, when converted to decimals, result in repeating decimals – decimals with a sequence of digits that repeat infinitely. For example, 1/3 = 0.3333...
When expressing these as percentages, you'll need to round the decimal to a certain number of decimal places for practical purposes. For example, you might round 1/3 to 0.33 and then express it as 33%. The level of precision needed depends on the context.
Conclusion
Converting 2/5 to its decimal (0.4) and percentage (40%) equivalent is a straightforward process that involves division and multiplication. Understanding these conversions is crucial for navigating various aspects of daily life, from financial calculations to data interpretation. Mastering these fundamental concepts lays a strong foundation for more advanced mathematical and analytical skills. Remember to practice these conversions with different fractions to strengthen your understanding and build confidence in your mathematical abilities. By understanding fractions, decimals, and percentages, you unlock a world of practical applications and enhance your problem-solving skills in various contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2/5 As A Decimal And Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.