2 Equivalent Fractions For 1 2
News Co
Mar 22, 2025 · 5 min read
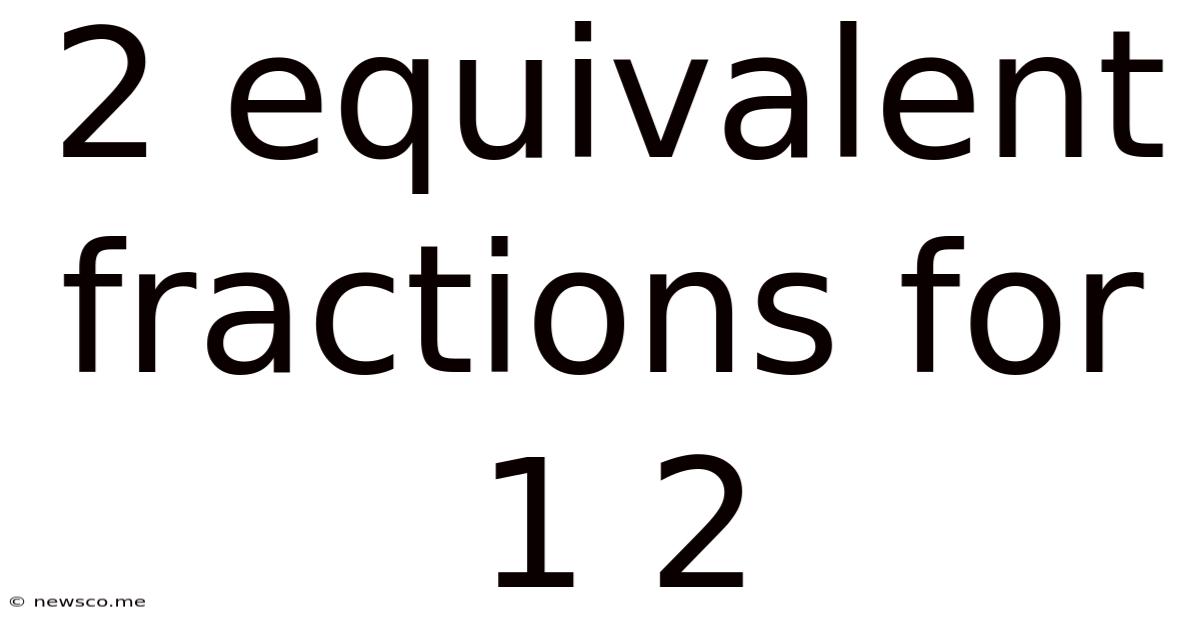
Table of Contents
2 Equivalent Fractions for 1 ½: A Deep Dive into Fraction Equivalence
Understanding fractions is a cornerstone of mathematical literacy. This article delves into the concept of equivalent fractions, specifically focusing on finding two equivalent fractions for the mixed number 1 ½. We'll explore the underlying principles, demonstrate multiple methods for finding these equivalent fractions, and discuss the practical applications of this crucial mathematical skill.
What are Equivalent Fractions?
Equivalent fractions represent the same portion of a whole, even though they look different. Imagine cutting a pizza into 4 slices and eating 2. You've eaten ½ the pizza. Now imagine cutting the same pizza into 8 slices. Eating 4 slices still represents ½ the pizza. ½ and ⁴⁄₈ are equivalent fractions because they both represent the same amount. The key is that the ratio between the numerator (top number) and the denominator (bottom number) remains constant.
Converting Mixed Numbers to Improper Fractions
Before we find equivalent fractions for 1 ½, we need to convert this mixed number into an improper fraction. A mixed number has a whole number part and a fractional part (e.g., 1 ½). An improper fraction has a numerator larger than or equal to its denominator (e.g., 3/2).
To convert 1 ½ to an improper fraction:
- Multiply the whole number by the denominator: 1 * 2 = 2
- Add the numerator: 2 + 1 = 3
- Keep the same denominator: The denominator remains 2.
Therefore, 1 ½ is equivalent to the improper fraction ³⁄₂. This is a crucial first step in finding equivalent fractions.
Method 1: Multiplying the Numerator and Denominator by the Same Number
The simplest method to find equivalent fractions is to multiply both the numerator and the denominator by the same non-zero number. This maintains the ratio and, therefore, the value of the fraction.
Let's find two equivalent fractions for ³⁄₂:
-
Multiply by 2:
- Numerator: 3 * 2 = 6
- Denominator: 2 * 2 = 4
- Equivalent fraction: ⁶⁄₄
-
Multiply by 3:
- Numerator: 3 * 3 = 9
- Denominator: 2 * 3 = 6
- Equivalent fraction: ⁹⁄₆
Therefore, two equivalent fractions for 1 ½ (or ³⁄₂) are ⁶⁄₄ and ⁹⁄₆. You can continue this process to find infinitely many equivalent fractions. Simply choose any non-zero whole number to multiply both the numerator and denominator.
Visual Representation of Equivalent Fractions
Consider a visual representation to solidify the understanding. Imagine a rectangle divided into two equal parts. Shading one and a half parts represents ³⁄₂. Now, imagine dividing each of those two parts into two smaller parts. You now have four parts, and shading three of them (⁶⁄₄) represents the same area as the initial one and a half parts. The same logic applies to dividing the initial two parts into three smaller parts (resulting in ⁹⁄₆). The visual representation helps to concretely illustrate the concept of equivalent fractions.
Method 2: Dividing the Numerator and Denominator by the Same Number (Simplification)
While the previous method creates equivalent fractions with larger numerators and denominators, we can also use division to find equivalent fractions with smaller numerators and denominators. This process is known as simplification or reducing to the lowest terms. Though we started with ³⁄₂, it's already in its simplest form as the greatest common divisor (GCD) of 3 and 2 is 1. However, let's illustrate this method with a different equivalent fraction, such as ⁹⁄₆.
The GCD of 9 and 6 is 3. Dividing both the numerator and denominator by 3:
- Numerator: 9 / 3 = 3
- Denominator: 6 / 3 = 2
- Simplified fraction: ³⁄₂
This demonstrates that ⁹⁄₆ simplifies to ³⁄₂, confirming its equivalence to 1 ½. Simplification is crucial for representing fractions in their most concise form.
Practical Applications of Equivalent Fractions
Understanding and working with equivalent fractions is crucial in many real-world applications:
-
Cooking and Baking: Recipes often require fractional measurements. Knowing equivalent fractions allows for flexibility in ingredient quantities. For instance, if a recipe calls for ½ cup of sugar, you could use ²/₄ cup or ⁴⁄₈ cup, depending on your measuring tools.
-
Measurement and Construction: Precision is paramount in fields like construction and engineering. Converting fractions to equivalent fractions with smaller or larger denominators is necessary for accurate measurements and calculations.
-
Finance: Working with percentages and proportions often involves using fractions. Understanding equivalent fractions helps in making accurate financial calculations, whether it's dealing with interest rates or calculating profits and losses.
-
Data Analysis: When analyzing data represented in fractions, understanding equivalence allows for easier comparisons and interpretations of different sets of data.
-
Sewing and Tailoring: Patterns and measurements frequently involve fractions. Equivalent fractions help ensure accurate cutting and stitching, leading to precise garment creation.
Beyond the Basics: Exploring Further Concepts
While finding two equivalent fractions for 1 ½ is a foundational skill, it opens the door to more complex fractional concepts:
-
Comparing Fractions: Understanding equivalent fractions helps in comparing fractions with different denominators. By converting fractions to equivalent fractions with a common denominator, we can easily determine which fraction is larger or smaller.
-
Adding and Subtracting Fractions: Adding and subtracting fractions with unlike denominators necessitates converting them to equivalent fractions with a common denominator. This ensures that we are adding or subtracting the same fractional parts.
-
Multiplying and Dividing Fractions: While not directly involving equivalent fractions in the same way as addition and subtraction, the concept of simplifying fractions after multiplication or division utilizes the idea of reducing to the lowest terms, which is a direct application of finding equivalent fractions.
-
Ratios and Proportions: Equivalent fractions are inherently linked to ratios and proportions. They are a fundamental tool in solving problems related to these concepts.
Conclusion: Mastering Equivalent Fractions
The ability to identify and work with equivalent fractions is a vital skill that underpins many mathematical operations and real-world applications. By understanding the underlying principles and employing different methods, such as multiplying or dividing the numerator and denominator by the same number, we can confidently find equivalent fractions for any given fraction, including 1 ½. Mastering this skill not only enhances your mathematical abilities but also equips you with a valuable tool for solving problems across various fields. The examples and explanations provided in this article aim to provide a comprehensive understanding of equivalent fractions, fostering confidence and competence in this fundamental mathematical concept. Remember that practice is key; continue exploring different fractions and applying these methods to strengthen your understanding and problem-solving skills. The more you practice, the more intuitive and effortless working with fractions will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 Equivalent Fractions For 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.