2 More Than 3 Times A Number X Is 17
News Co
May 08, 2025 · 4 min read
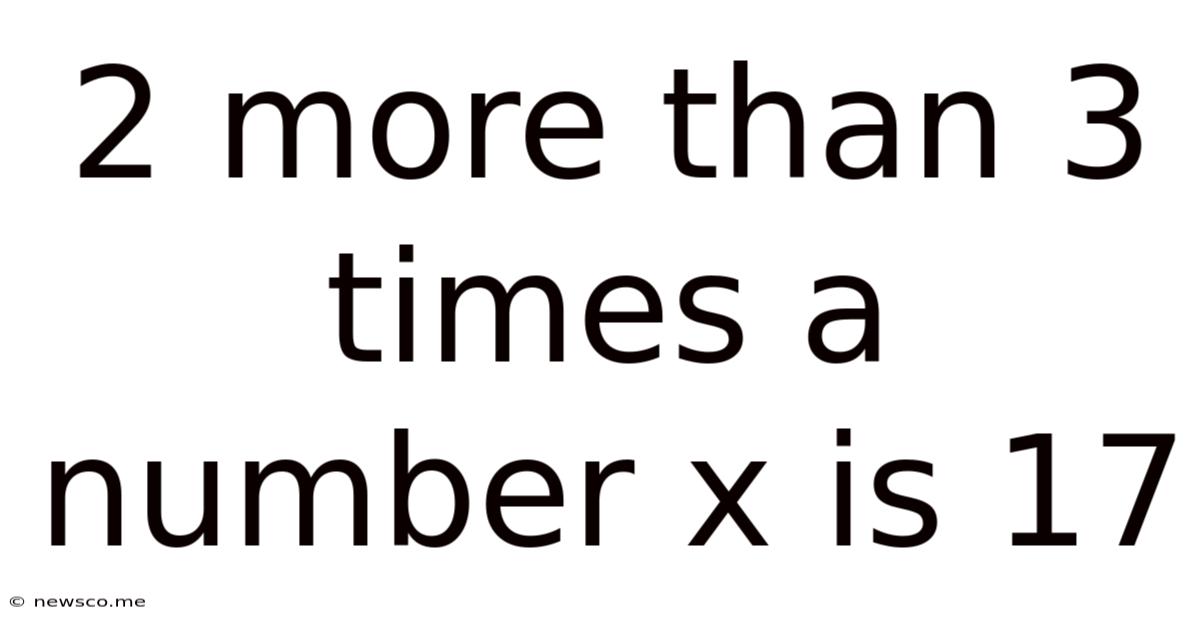
Table of Contents
2 More Than 3 Times a Number x is 17: A Deep Dive into Equation Solving
This seemingly simple equation, "2 more than 3 times a number x is 17," opens the door to a fascinating exploration of algebraic principles, problem-solving strategies, and the interconnectedness of mathematical concepts. While the solution itself is straightforward, understanding the underlying mechanics and exploring related concepts significantly enhances mathematical comprehension and problem-solving skills. Let's delve into this equation and uncover its hidden depths.
Understanding the Problem: Deconstructing the Equation
The statement "2 more than 3 times a number x is 17" can be directly translated into an algebraic equation. Let's break down each part:
- "a number x": This represents our unknown variable, denoted by 'x'.
- "3 times a number x": This translates to 3 * x, or more concisely, 3x.
- "2 more than 3 times a number x": This signifies adding 2 to the previous expression, resulting in 3x + 2.
- "is 17": This indicates that the entire expression is equal to 17.
Therefore, the complete algebraic representation of the problem is:
3x + 2 = 17
Solving the Equation: A Step-by-Step Approach
Solving for 'x' involves isolating the variable on one side of the equation. We achieve this by performing inverse operations. The steps are as follows:
-
Subtract 2 from both sides: This cancels out the '+2' on the left side, leaving us with:
3x = 15
-
Divide both sides by 3: This isolates 'x' by canceling out the multiplication by 3:
x = 5
Therefore, the solution to the equation is x = 5.
Verification: Checking the Solution
It's crucial to verify our solution. We substitute 'x = 5' back into the original equation:
3(5) + 2 = 15 + 2 = 17
Since the equation holds true, our solution, x = 5, is correct.
Expanding the Horizons: Exploring Related Concepts
While solving the equation is straightforward, exploring related concepts deepens our understanding of algebra and its applications:
1. Different Representations of the Problem
The problem can be expressed in various ways, all leading to the same equation:
- "Three times a number increased by two equals seventeen."
- "The sum of twice a number and fifteen is seventeen." (This requires a slightly different initial algebraic setup but leads to the same solution).
- "What number, when multiplied by three and then increased by two, results in seventeen?"
Understanding these different formulations enhances problem-solving flexibility.
2. Visualizing the Equation: Geometric Interpretation
The equation 3x + 2 = 17 can be visualized geometrically. Imagine a rectangle with a length of 3x and a width of 1. Adding a 2 x 1 rectangle to it represents the '+2'. The total area of this combined shape is 17. Solving the equation then becomes finding the length 'x' that satisfies this area constraint.
3. Real-World Applications
This type of equation frequently appears in real-world scenarios. For instance:
- Cost Calculation: If a product costs 3x dollars and a 2-dollar shipping fee is added, and the total cost is 17 dollars, the equation helps determine the cost of the product (x).
- Distance Problems: If a car travels 3x kilometers and an additional 2 kilometers, and the total distance is 17 kilometers, the equation helps determine the initial distance (x).
- Profit Calculation: A business earns 3x dollars in profit and adds 2 dollars, totaling 17 dollars. The equation helps find the initial profit (x).
4. Generalizing the Equation: Exploring Parameters
We can generalize the equation to:
ax + b = c
Where 'a', 'b', and 'c' are constants. Solving this general form improves our ability to tackle similar problems with different numerical values. The solution for x would then be:
x = (c - b) / a
5. Inequalities: Extending the Concept
Instead of an equation, we can explore related inequalities:
- 3x + 2 > 17 (3x + 2 is greater than 17)
- 3x + 2 < 17 (3x + 2 is less than 17)
Solving these inequalities provides a range of values for 'x' rather than a single solution.
6. Systems of Equations: More Complex Scenarios
The equation can be integrated into a system of equations, involving multiple variables and equations. Solving these systems requires more advanced techniques but builds upon the fundamental principles learned from solving simple equations like 3x + 2 = 17.
7. Advanced Algebraic Techniques: Beyond Basic Solving
While this equation is solved through simple algebraic manipulation, more advanced techniques, such as substitution and elimination, are essential for more complex algebraic problems. Understanding the foundational concepts from simple equations paves the way for mastering more sophisticated algebraic methods.
Conclusion: Beyond the Numbers
The equation "2 more than 3 times a number x is 17" serves as more than just a simple algebraic exercise. It provides a springboard for understanding core algebraic concepts, exploring related mathematical ideas, and developing problem-solving skills. By analyzing the equation from different perspectives and applying it to real-world scenarios, we gain a deeper appreciation for the power and versatility of algebra and its crucial role in various fields. The journey from a simple equation to a broader mathematical understanding exemplifies the beauty and interconnectedness of mathematical principles. Mastering this seemingly simple concept forms a strong foundation for tackling more complex mathematical challenges and applying mathematical thinking to real-world problem-solving.
Latest Posts
Latest Posts
-
How Many Times Does 16 Go Into 80
May 08, 2025
-
Function A And Function B Are Linear Functions
May 08, 2025
-
The Square Surface Shown In The Figure Measures
May 08, 2025
-
Is The Square Root Of 42 Rational Or Irrational
May 08, 2025
-
What Is The Greatest Common Factor Of 56 And 96
May 08, 2025
Related Post
Thank you for visiting our website which covers about 2 More Than 3 Times A Number X Is 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.