2 Out Of 8 Is What Percent
News Co
Mar 23, 2025 · 5 min read
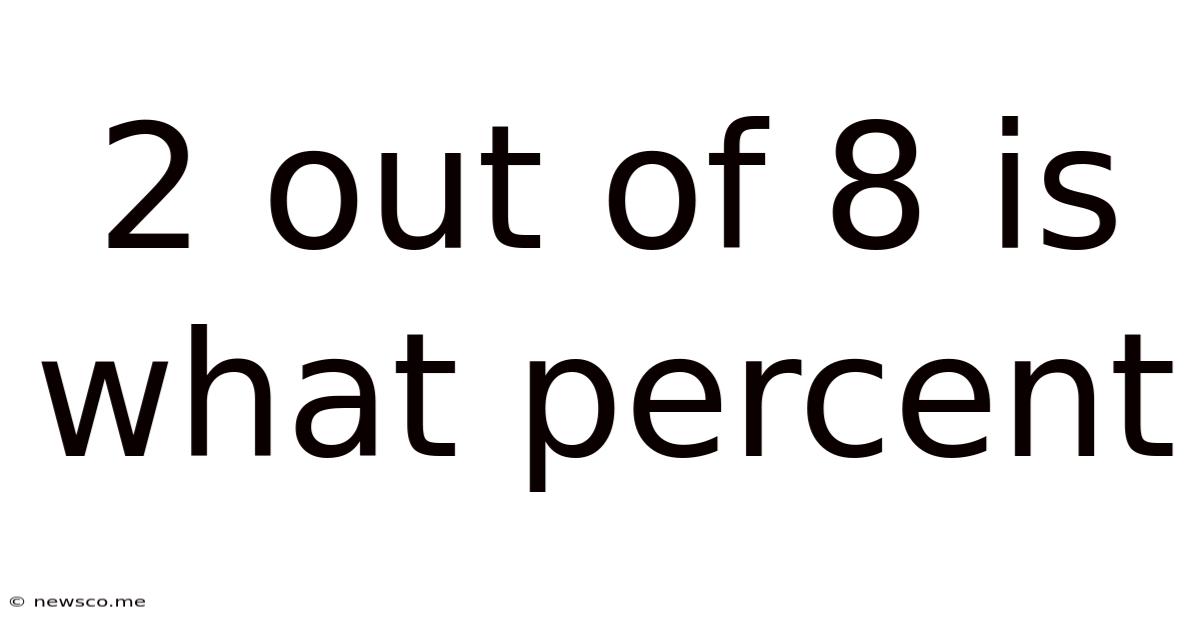
Table of Contents
2 Out of 8 is What Percent? A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will delve into the question, "2 out of 8 is what percent?", exploring different methods of calculation, practical applications, and extending the concept to more complex scenarios. We'll also touch upon the importance of percentage calculations in everyday life and various professional fields.
Understanding the Fundamentals of Percentages
Before we tackle the specific problem, let's refresh our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 50% means 50 out of 100, which can be simplified to 1/2 or 0.5 as a decimal.
Key Terms and Concepts
- Numerator: The top number in a fraction (in our case, 2). This represents the part.
- Denominator: The bottom number in a fraction (in our case, 8). This represents the whole.
- Percentage: The fraction expressed as a value out of 100.
Calculating "2 out of 8" as a Percentage: Three Methods
There are several ways to calculate what percentage 2 out of 8 represents. Let's explore three common methods:
Method 1: Using the Fraction Method
This is perhaps the most straightforward approach. We start by expressing the given information as a fraction:
2/8
Next, we simplify the fraction:
2/8 = 1/4
Now, we need to convert this fraction into a percentage. To do this, we divide the numerator by the denominator and then multiply the result by 100:
(1 ÷ 4) × 100 = 0.25 × 100 = 25%
Therefore, 2 out of 8 is 25%.
Method 2: Using Proportions
This method involves setting up a proportion to solve for the unknown percentage. We can represent the problem as:
2/8 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
8x = 200
Now, divide both sides by 8:
x = 200 ÷ 8 = 25
Therefore, x = 25%, confirming our previous result. This method is particularly useful when dealing with more complex percentage problems.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply divide the numerator (2) by the denominator (8) and then multiply the result by 100. This gives you the same answer: 25%. This method is the quickest and most efficient for simple percentage calculations.
Practical Applications of Percentage Calculations
Understanding percentages is crucial in many real-world scenarios. Here are some examples:
1. Sales and Discounts:
Retail stores frequently advertise discounts as percentages. For example, a "25% off" sale means you pay 75% of the original price. Knowing how to calculate percentages helps you determine the final price after a discount.
2. Taxes:
Sales tax, income tax, and other taxes are expressed as percentages. Calculating the tax amount requires understanding percentage calculations.
3. Financial Analysis:
In finance, percentages are used to analyze investment returns, interest rates, and profit margins. Understanding percentages is essential for making informed financial decisions.
4. Data Analysis and Statistics:
Percentages are frequently used to represent data in charts, graphs, and reports. This helps visualize trends and patterns in data. For instance, analyzing survey results often involves calculating percentages of respondents who chose certain options.
5. Academic Performance:
Grade point averages (GPAs) are often expressed as percentages, providing a standardized measure of academic performance.
6. Scientific Research:
In scientific research, percentages are used to express experimental results, error margins, and statistical significance.
Extending the Concept: More Complex Percentage Problems
While the "2 out of 8" example is relatively simple, the principles can be applied to more complex scenarios. Let's consider some examples:
Example 1: Finding the percentage increase or decrease:
Suppose a stock price increases from $50 to $60. To find the percentage increase, follow these steps:
- Find the difference: $60 - $50 = $10
- Divide the difference by the original amount: $10/$50 = 0.2
- Multiply by 100 to express as a percentage: 0.2 × 100 = 20%
Therefore, the stock price increased by 20%.
Example 2: Calculating percentage composition:
Imagine a mixture containing 10 grams of substance A and 30 grams of substance B. To find the percentage composition of substance A:
- Find the total mass: 10g + 30g = 40g
- Divide the mass of substance A by the total mass: 10g/40g = 0.25
- Multiply by 100 to express as a percentage: 0.25 × 100 = 25%
Substance A makes up 25% of the mixture.
Example 3: Working backwards from a percentage:
If you know that 30% of a number is 60, you can find the original number by setting up a proportion:
30/100 = 60/x
Cross-multiplying and solving for x gives you x = 200.
These examples demonstrate the versatility of percentage calculations and their applicability to a wide range of problems.
Mastering Percentages: Tips and Tricks
- Practice Regularly: The best way to master percentages is through consistent practice. Solve various problems to build your understanding and confidence.
- Visual Aids: Utilize visual aids like charts and diagrams to better grasp the concept.
- Real-World Applications: Apply percentage calculations to your everyday life to reinforce your learning.
- Use Online Resources: Numerous online resources, including calculators and tutorials, can assist in learning and practicing percentage calculations.
Conclusion: The Importance of Percentage Literacy
The ability to understand and calculate percentages is a critical life skill. From managing personal finances to interpreting data in professional settings, percentages are an integral part of everyday life. Mastering this skill opens up opportunities for better decision-making, improved problem-solving abilities, and a deeper understanding of the world around us. By understanding the various methods of calculating percentages and applying them to different scenarios, you can confidently tackle any percentage-related challenge that comes your way. Remember to practice regularly and apply your knowledge to real-world situations to solidify your understanding and enhance your numeracy skills. Understanding "2 out of 8 is what percent?" is just the beginning of your journey towards percentage mastery.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 Out Of 8 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.