2 Over 6 In Simplest Form
News Co
Mar 30, 2025 · 5 min read
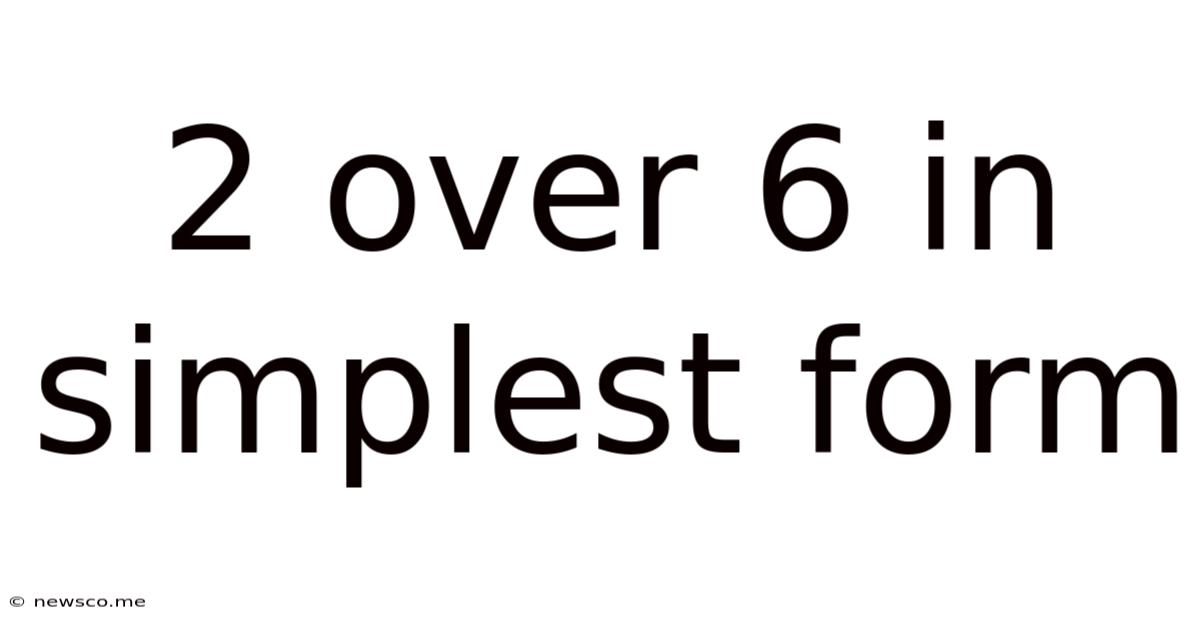
Table of Contents
2 Over 6 in Simplest Form: A Comprehensive Guide to Fraction Simplification
Understanding fractions is fundamental to mathematics, and simplifying fractions is a crucial skill for various applications. This comprehensive guide delves into the simplification of the fraction 2/6, providing a step-by-step approach, exploring underlying concepts, and offering real-world examples. We'll cover various methods, catering to different learning styles and ensuring a thorough understanding of the process.
What Does "Simplest Form" Mean?
Before we dive into simplifying 2/6, let's clarify what "simplest form" means in the context of fractions. A fraction is in its simplest form, also known as its lowest terms, when the greatest common divisor (GCD) of the numerator (the top number) and the denominator (the bottom number) is 1. In simpler terms, this means there's no whole number (other than 1) that can divide both the numerator and the denominator evenly.
Finding the Greatest Common Divisor (GCD)
The key to simplifying fractions lies in finding the GCD of the numerator and denominator. There are several ways to find the GCD:
1. Listing Factors:
This method involves listing all the factors of both the numerator and the denominator and identifying the largest factor they have in common.
- Factors of 2: 1, 2
- Factors of 6: 1, 2, 3, 6
The largest common factor is 2.
2. Prime Factorization:
This method involves expressing both the numerator and the denominator as a product of their prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
- Prime factorization of 2: 2 (2 is itself a prime number)
- Prime factorization of 6: 2 x 3
The common prime factor is 2.
3. Euclidean Algorithm:
This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's apply the Euclidean algorithm to 2 and 6:
- Divide 6 by 2: 6 = 2 x 3 + 0
- The remainder is 0, so the GCD is the last non-zero remainder, which is 2.
Simplifying 2/6
Now that we understand how to find the GCD, let's simplify 2/6:
We've determined that the GCD of 2 and 6 is 2. To simplify the fraction, we divide both the numerator and the denominator by the GCD:
2 ÷ 2 / 6 ÷ 2 = 1/3
Therefore, the simplest form of 2/6 is 1/3.
Visual Representation of Fraction Simplification
It's often helpful to visualize fraction simplification. Imagine you have a pizza cut into 6 slices. If you have 2 slices (2/6 of the pizza), you have one-third (1/3) of the whole pizza. This visual representation reinforces the equivalence between 2/6 and 1/3.
Understanding Equivalent Fractions
Simplifying a fraction doesn't change its value; it just expresses it in a more concise and manageable form. 2/6 and 1/3 are equivalent fractions; they represent the same portion or quantity. You can obtain equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number.
For example:
- 1/3 x 2/2 = 2/6
- 1/3 x 3/3 = 3/9
- 1/3 x 4/4 = 4/12
All these fractions (1/3, 2/6, 3/9, 4/12 etc.) are equivalent, but 1/3 is the simplest form.
Real-World Applications of Fraction Simplification
Simplifying fractions is not just an academic exercise; it has practical applications in various real-world scenarios:
-
Cooking and Baking: Recipes often use fractions. Simplifying fractions makes it easier to measure ingredients accurately. For example, if a recipe calls for 2/6 of a cup of sugar, it's easier to measure 1/3 of a cup.
-
Construction and Engineering: Engineers and architects use fractions extensively in their calculations. Simplifying fractions ensures accuracy and efficiency in their work.
-
Finance and Budgeting: Fractions are used in calculating percentages, interest rates, and proportions in financial planning and budgeting. Simplifying fractions makes financial calculations easier to understand and interpret.
-
Data Analysis: Fractions are often used to represent data and proportions in data analysis. Simplifying fractions makes it easier to interpret and present data effectively.
Common Mistakes to Avoid When Simplifying Fractions
While simplifying fractions is a relatively straightforward process, some common mistakes can lead to incorrect results.
-
Dividing only the numerator or denominator: Remember that you must divide both the numerator and the denominator by the GCD to maintain the value of the fraction. Dividing only one will result in an incorrect equivalent fraction.
-
Incorrectly identifying the GCD: Carefully determine the GCD using one of the methods outlined above. An incorrect GCD will lead to an incorrectly simplified fraction.
-
Not simplifying completely: Make sure to divide by the greatest common divisor. If you divide by a smaller common factor, you may not arrive at the simplest form.
Advanced Fraction Simplification Techniques
For more complex fractions, or fractions with larger numbers, more advanced techniques can be helpful:
-
Using prime factorization for larger numbers: This is especially useful when dealing with numbers that have many factors.
-
Utilizing the Euclidean Algorithm: As mentioned earlier, this is a more efficient algorithm for larger numbers, avoiding the need to list all factors.
-
Using software or calculators: For very complex fractions or for checking your work, you can use mathematical software or calculators that have built-in fraction simplification tools.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a crucial skill with broad applications. By understanding the concepts of greatest common divisor, equivalent fractions, and applying appropriate methods, you can master the process and improve your problem-solving abilities in various mathematical contexts. Remember to practice regularly, and don't hesitate to use visual aids or different techniques to find the approach that works best for you. With consistent practice, you'll confidently simplify any fraction and gain a deeper understanding of this essential mathematical concept. The seemingly simple task of simplifying 2/6 to 1/3 lays the foundation for more complex mathematical manipulations and problem-solving in numerous fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 Over 6 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.