2 X 2 X 2 X 3
News Co
Mar 15, 2025 · 5 min read
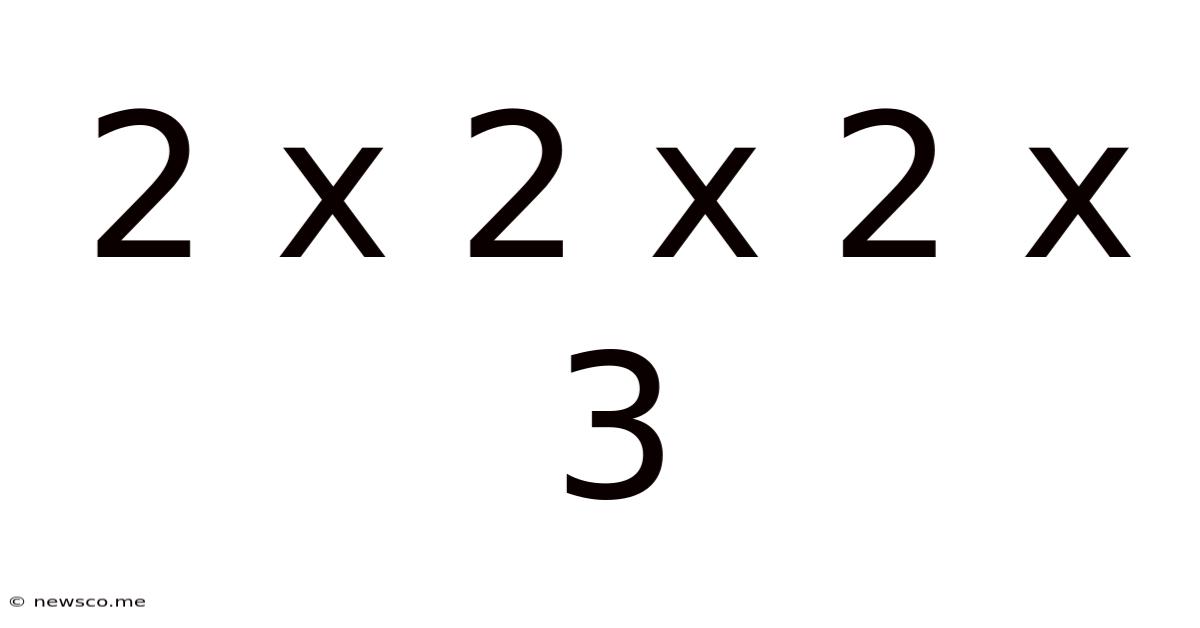
Table of Contents
Decomposing 2 x 2 x 2 x 3: A Deep Dive into Prime Factorization and its Applications
The seemingly simple expression "2 x 2 x 2 x 3" offers a fascinating gateway into the world of mathematics, specifically the concepts of prime factorization, number theory, and their far-reaching applications in various fields. This seemingly simple calculation, resulting in 24, unlocks a wealth of mathematical exploration. Let's delve into this number's properties and significance, exploring its underlying structure and practical implications.
Understanding Prime Factorization
At the heart of understanding 2 x 2 x 2 x 3 lies the concept of prime factorization. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Prime numbers are the fundamental building blocks of all other whole numbers. The prime factorization of a number is the unique representation of that number as a product of its prime factors.
In our case, 24 (2 x 2 x 2 x 3) is elegantly expressed in its prime factorization. The numbers 2 and 3 are both prime numbers. This factorization tells us that 24 can be constructed solely from the multiplication of these two prime numbers. This unique decomposition is crucial in various mathematical contexts.
The Importance of Uniqueness: The Fundamental Theorem of Arithmetic guarantees that every integer greater than 1 can be represented as a unique product of prime numbers (ignoring the order of the factors). This uniqueness is a cornerstone of many mathematical proofs and algorithms.
Exploring the Properties of 24
The prime factorization of 24 (2³ x 3) immediately reveals several key properties:
-
Divisors: Knowing the prime factorization allows us to easily determine all the divisors of 24. The divisors are all possible combinations of the prime factors: 1, 2, 3, 4, 6, 8, 12, and 24. This is invaluable in number theory and applications involving divisibility.
-
Even Number: The presence of the prime factor 2 (cubed, even) immediately signifies that 24 is an even number. Even numbers are divisible by 2.
-
Composite Number: Since 24 has prime factors other than itself and 1, it's a composite number – a whole number that can be divided evenly by numbers other than 1 and itself.
-
Factors and Multiples: The prime factorization is also crucial in identifying factors (numbers that divide 24 evenly) and multiples (numbers that are divisible by 24).
Applications of Prime Factorization and the Number 24
The seemingly simple number 24, and its prime factorization, has surprisingly widespread applications in various fields:
1. Cryptography
Prime numbers are the bedrock of modern cryptography. Algorithms like RSA encryption rely heavily on the difficulty of factoring large numbers into their prime components. The larger the numbers, the more computationally intensive the factorization becomes, ensuring data security. While 24 is trivially factored, the principle extends to vastly larger numbers used in secure communication systems.
2. Computer Science
Prime factorization algorithms are essential in computer science for tasks like generating unique identifiers, hash functions, and optimizing certain types of computations. The efficiency of these algorithms directly impacts the performance of many computer systems.
3. Combinatorics and Probability
In combinatorics and probability, prime factorization helps in solving problems related to permutations, combinations, and the distribution of probabilities. The number of divisors, readily derived from the prime factorization, often plays a critical role in counting possibilities. For example, the number of ways to arrange objects or the likelihood of certain events can be elegantly analyzed using prime factorization.
4. Music Theory
Surprisingly, the number 24 and its factors appear in music theory. 24 is a highly divisible number, leading to many musical subdivisions and rhythmic patterns. It's related to the number of major and minor keys in Western music and appears in various musical structures and compositions.
5. Geometry and Spatial Reasoning
In geometry, the number 24 often emerges in the context of polyhedra. For instance, the regular octahedron has 24 edges, a fact that relates directly to its symmetric properties and spatial arrangement. The number's properties influence geometric constructions and analyses.
6. Calendar Systems
The number 24, with its close relation to 12 (2 x 2 x 3), plays a role in calendar systems. We have 24 hours in a day, reflecting the significance of this highly composite number in the structure of time measurement. Its divisibility enables convenient subdivisions of time intervals.
Beyond 24: Expanding the Mathematical Landscape
While our focus has been on 2 x 2 x 2 x 3 = 24, understanding this simple factorization lays a strong foundation for grasping more complex mathematical concepts. Here are some extensions:
-
Exploring Larger Numbers: The principles of prime factorization extend to arbitrarily large numbers. The difficulty of factoring very large numbers is what underpins the security of many cryptographic systems.
-
Modular Arithmetic: Understanding the prime factorization of a number is crucial in modular arithmetic, a branch of mathematics used extensively in cryptography and computer science.
-
Number Theory: Prime factorization is a fundamental concept within number theory, a branch of mathematics dedicated to studying integers and their properties.
Conclusion: The Enduring Significance of a Simple Calculation
The seemingly mundane calculation 2 x 2 x 2 x 3 = 24 is far from simple when examined through the lens of mathematics. It offers a gateway into prime factorization, a fundamental concept with far-reaching implications in cryptography, computer science, music theory, geometry, and many other fields. This simple calculation demonstrates the power of mathematical exploration and the hidden depths contained within seemingly straightforward numerical expressions. The unique properties of 24, directly resulting from its prime factorization, underline its importance in various contexts, highlighting the interconnectedness of mathematical concepts and their relevance to the wider world. This exploration should encourage further investigation into the fascinating world of numbers and their hidden relationships.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 2 X 2 X 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.