2 X 2 X 3 X 3
News Co
Mar 19, 2025 · 5 min read
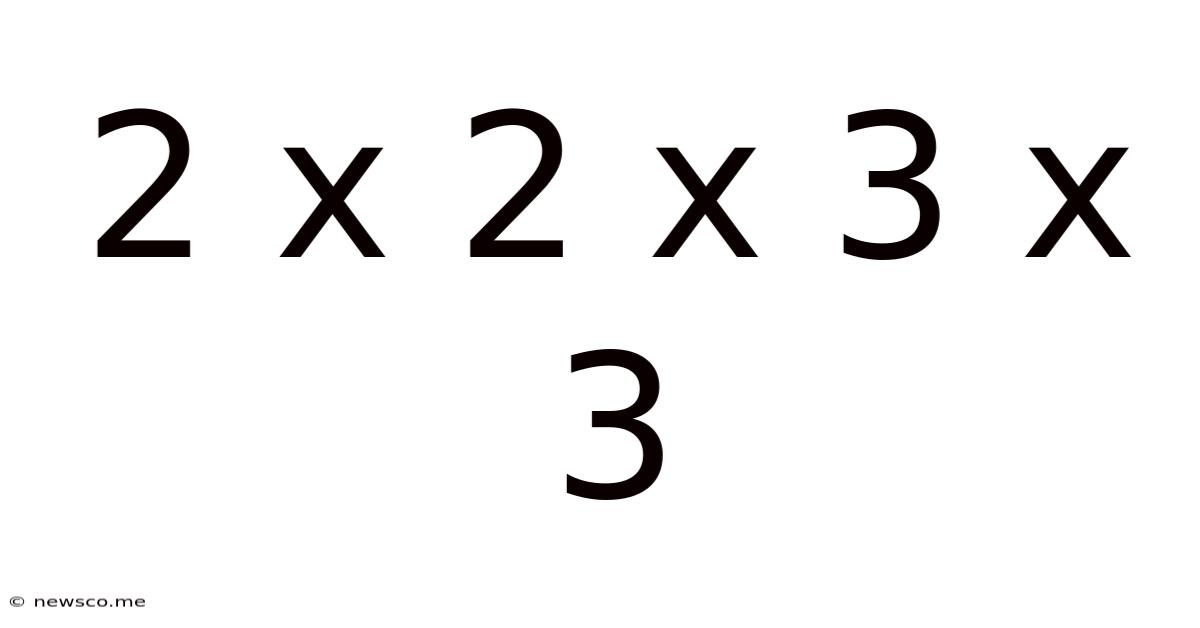
Table of Contents
- 2 X 2 X 3 X 3
- Table of Contents
- Decoding 2 x 2 x 3 x 3: A Deep Dive into Multiplication, Factorization, and Beyond
- Understanding the Fundamentals: Multiplication
- Prime Factorization: Unveiling the Building Blocks
- The Significance of Prime Factorization
- Exploring Exponents and Powers
- Beyond the Basics: Applications of 2 x 2 x 3 x 3
- Expanding the Scope: Related Mathematical Concepts
- Conclusion: The Unassuming Power of 2 x 2 x 3 x 3
- Latest Posts
- Related Post
Decoding 2 x 2 x 3 x 3: A Deep Dive into Multiplication, Factorization, and Beyond
The seemingly simple expression "2 x 2 x 3 x 3" opens a door to a surprisingly rich world of mathematical concepts. While the answer itself is straightforward (36), the journey to understanding its implications delves into fundamental mathematical principles like multiplication, factorization, prime numbers, and even touches upon more advanced topics. This article will explore this seemingly simple equation in detail, uncovering its hidden mathematical depths and showcasing its relevance in various mathematical contexts.
Understanding the Fundamentals: Multiplication
At its core, "2 x 2 x 3 x 3" represents repeated multiplication. Multiplication is a fundamental arithmetic operation that signifies repeated addition. For instance, 2 x 2 can be visualized as adding two groups of two (2 + 2 = 4). Extending this to our expression, we perform a series of multiplications:
- Step 1: 2 x 2 = 4. This represents two groups of two.
- Step 2: 4 x 3 = 12. Now we have three groups of four.
- Step 3: 12 x 3 = 36. Finally, we have three groups of twelve.
This sequential process illustrates the associative property of multiplication, which states that the grouping of factors does not affect the final product. We could have just as easily calculated:
- (2 x 2) x (3 x 3) = 4 x 9 = 36
- 2 x (2 x 3) x 3 = 2 x 6 x 3 = 36
- 2 x 2 x (3 x 3) = 4 x 9 = 36
This flexibility highlights the power and elegance of multiplication.
Prime Factorization: Unveiling the Building Blocks
The expression "2 x 2 x 3 x 3" also provides a perfect illustration of prime factorization. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. The numbers 2 and 3 are prime numbers. Prime factorization is the process of expressing a number as a product of its prime factors. In our case, 36 can be uniquely expressed as 2 x 2 x 3 x 3, or more concisely as 2² x 3².
This prime factorization is unique to 36. No other combination of prime numbers will multiply to give 36. This fundamental theorem of arithmetic is crucial in various areas of mathematics, including cryptography and number theory.
The Significance of Prime Factorization
The ability to break down a number into its prime factors is extremely useful for several reasons:
- Simplifying Fractions: Prime factorization helps simplify fractions by identifying common factors in the numerator and denominator.
- Finding the Greatest Common Divisor (GCD): By comparing the prime factorizations of two numbers, we can easily find their GCD, the largest number that divides both without leaving a remainder.
- Finding the Least Common Multiple (LCM): Similarly, prime factorization allows us to determine the LCM, the smallest number that is a multiple of both numbers.
- Solving Equations: In advanced algebra and number theory, prime factorization plays a crucial role in solving complex equations and proving theorems.
Exploring Exponents and Powers
The prime factorization of 36, expressed as 2² x 3², introduces the concept of exponents. Exponents represent repeated multiplication of the same number. In 2², the exponent 2 indicates that 2 is multiplied by itself twice (2 x 2 = 4). Similarly, 3² means 3 multiplied by itself twice (3 x 3 = 9).
Understanding exponents is essential for:
- Scientific Notation: Exponents are vital in representing very large or very small numbers concisely in scientific notation.
- Polynomial Expressions: Exponents are fundamental to algebraic expressions, including polynomials.
- Exponential Functions: Exponents form the basis of exponential functions which model many real-world phenomena, such as population growth and radioactive decay.
Beyond the Basics: Applications of 2 x 2 x 3 x 3
While seemingly simple, the expression "2 x 2 x 3 x 3" and the concepts it embodies have numerous applications across various mathematical fields and real-world scenarios:
-
Geometry: The number 36 could represent the area of a square with side length 6 (6 x 6 = 36). It could also represent the number of square units in a rectangle with dimensions 4 x 9 or 3 x 12. Understanding factor pairs is essential in solving geometric problems related to area and volume.
-
Combinatorics: In combinatorics, which deals with counting, 36 could represent the number of possible outcomes in various scenarios. For instance, if you have four shirts and nine pairs of pants, you have 36 different outfits (4 x 9 = 36).
-
Probability: Understanding prime factorization can be helpful in calculating probabilities, especially when dealing with events that are independent and mutually exclusive.
Expanding the Scope: Related Mathematical Concepts
Let's broaden our exploration by considering some closely related mathematical concepts:
-
Factors and Multiples: The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36. The multiples of 36 are 36, 72, 108, 144, and so on. Understanding the relationship between factors and multiples is crucial in simplifying fractions, finding common denominators, and solving various mathematical problems.
-
Square Numbers: 36 is a perfect square (6 x 6 = 36). Perfect squares are numbers that can be obtained by squaring a whole number. Understanding perfect squares is important in geometry (areas of squares), algebra (solving quadratic equations), and number theory.
-
Divisibility Rules: Knowing the divisibility rules for 2, 3, and other numbers can help quickly determine if 36 (or any number) is divisible by specific numbers without performing the actual division. For instance, 36 is divisible by 2 because it's an even number, and it's divisible by 3 because the sum of its digits (3 + 6 = 9) is divisible by 3.
Conclusion: The Unassuming Power of 2 x 2 x 3 x 3
The simple expression "2 x 2 x 3 x 3" serves as a gateway to a vast landscape of mathematical concepts. From basic arithmetic operations like multiplication to advanced topics such as prime factorization, exponents, and divisibility rules, this seemingly straightforward equation underscores the interconnectedness and beauty of mathematics. Understanding its underlying principles offers a firm foundation for tackling more complex mathematical challenges and opens doors to appreciating the elegance and power inherent in even the simplest mathematical expressions. By exploring its various facets, we gain a deeper understanding of the fundamental building blocks of mathematics and their wide-ranging applications in the world around us. The unassuming power of 2 x 2 x 3 x 3 lies not just in its numerical result, but in the rich tapestry of mathematical concepts it unveils.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 X 2 X 3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.