20 3 As A Mixed Number
News Co
May 07, 2025 · 4 min read
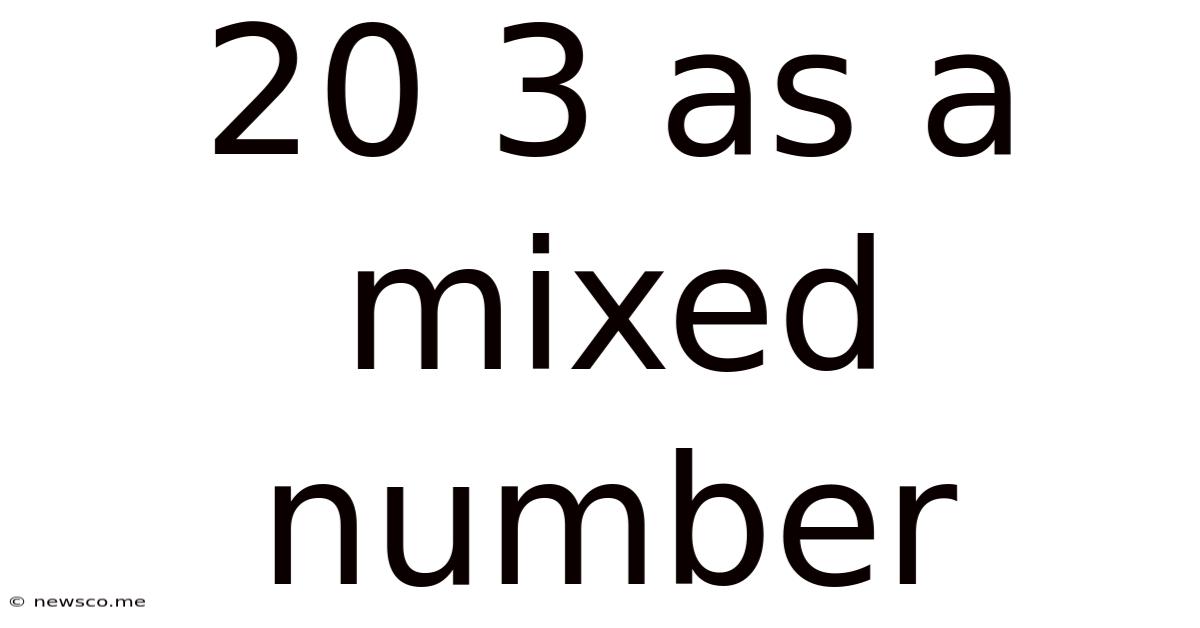
Table of Contents
20/3 as a Mixed Number: A Comprehensive Guide
Understanding fractions and their conversion into mixed numbers is a fundamental concept in mathematics. This comprehensive guide delves into the process of converting the improper fraction 20/3 into a mixed number, explaining the underlying principles and providing practical examples. We'll explore different methods, address common misconceptions, and even touch upon the applications of this conversion in real-world scenarios.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (top number) is smaller than the denominator (bottom number). For instance, 1 ¾, 2 ⅔, and 5 ⅛ are all examples of mixed numbers. They represent a quantity that is greater than one whole unit.
Converting Improper Fractions to Mixed Numbers
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. 20/3 is an improper fraction because 20 (numerator) is larger than 3 (denominator). Converting an improper fraction to a mixed number involves dividing the numerator by the denominator.
The Division Method: Step-by-Step Guide
-
Divide the numerator by the denominator: Divide 20 by 3. This gives us a quotient (the result of the division) and a remainder.
20 ÷ 3 = 6 with a remainder of 2
-
The quotient becomes the whole number part: The quotient, 6, becomes the whole number part of our mixed number.
-
The remainder becomes the numerator of the fraction: The remainder, 2, becomes the numerator of the fractional part.
-
The denominator remains the same: The denominator remains the same as the original fraction, which is 3.
Therefore, 20/3 as a mixed number is 6⅔.
Visualizing the Conversion
Imagine you have 20 identical objects, and you want to group them into sets of 3. You can form 6 complete sets of 3, with 2 objects remaining. This visually represents the 6 whole units (the quotient) and the remaining 2/3 (the remainder).
Understanding the Relationship Between Improper Fractions and Mixed Numbers
Improper fractions and mixed numbers represent the same quantity, just expressed differently. They are interchangeable. Knowing how to convert between them is essential for various mathematical operations and problem-solving.
Practical Applications of Converting 20/3 to a Mixed Number
The conversion of improper fractions to mixed numbers has numerous applications in everyday life and various fields:
-
Measurement: Imagine measuring the length of a piece of wood. If the measurement is 20/3 meters, converting it to the mixed number 6⅔ meters makes it easier to visualize and understand.
-
Cooking and Baking: Recipes often use fractions. Converting improper fractions to mixed numbers allows for easier comprehension and measurement of ingredients. A recipe calling for 20/3 cups of flour is more easily understood as 6⅔ cups.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Converting improper fractions to mixed numbers simplifies calculations and minimizes errors.
-
Data Analysis: In statistics and data analysis, working with mixed numbers can be more intuitive than working with improper fractions, particularly when dealing with averages or representing data visually.
Alternative Methods for Conversion (for advanced understanding)
While the division method is the most straightforward, other methods can reinforce understanding:
-
Repeated Subtraction: Repeatedly subtract the denominator (3) from the numerator (20) until you get a number less than the denominator. The number of times you subtract is the whole number part, and the remainder is the numerator of the fraction.
-
Using a Number Line: Visualizing the improper fraction on a number line can help understand its equivalent mixed number representation.
Common Mistakes to Avoid
-
Forgetting the remainder: A frequent mistake is forgetting to include the remainder as the numerator of the fractional part of the mixed number.
-
Incorrect division: Errors in the division process can lead to an incorrect mixed number. Double-check your division work.
-
Misinterpreting the denominator: Ensure that you maintain the original denominator throughout the conversion process.
Further Exploration: Working with Larger Improper Fractions
The principles discussed for converting 20/3 apply to any improper fraction, no matter how large the numerator and denominator. The process remains consistent: divide the numerator by the denominator, use the quotient as the whole number, and the remainder as the numerator of the fraction. For larger numbers, using a calculator might be helpful for the division step, but understanding the underlying process is crucial.
Conclusion
Converting the improper fraction 20/3 to the mixed number 6⅔ is a fundamental mathematical skill with broad applications. By mastering this conversion, you enhance your understanding of fractions, improving your ability to solve problems in various contexts. The method is straightforward, yet understanding the underlying principles and practicing the techniques will solidify your grasp of this essential concept, enabling you to approach more complex mathematical challenges with confidence. Remember to always check your work and visualize the problem to enhance your comprehension.
Latest Posts
Related Post
Thank you for visiting our website which covers about 20 3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.