20 Is What Percent Of 15
News Co
Mar 20, 2025 · 4 min read
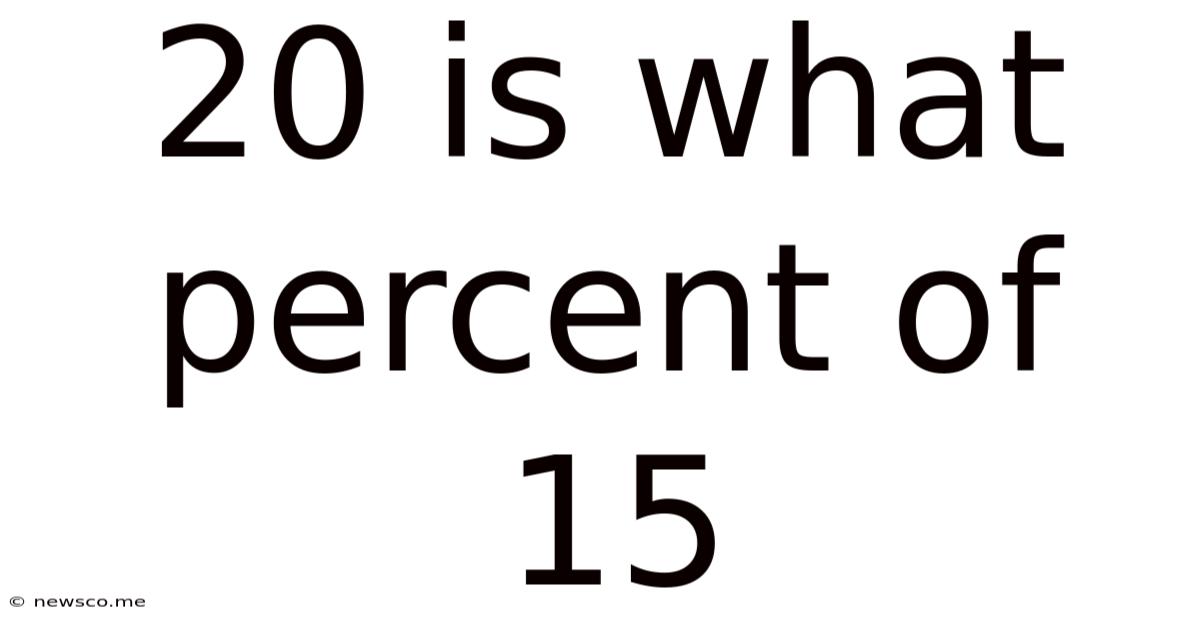
Table of Contents
20 is What Percent of 15? A Deep Dive into Percentage Calculations
This seemingly simple question, "20 is what percent of 15?", opens the door to a fascinating exploration of percentages, their applications, and the underlying mathematical principles. While the answer might seem immediately obvious to some, understanding the why behind the calculation is crucial for mastering this fundamental concept in mathematics and various real-world scenarios. This article will not only provide the solution but also delve into the method, its variations, and practical examples to solidify your understanding.
Understanding Percentages: The Foundation
Before tackling the specific problem, let's establish a solid understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be represented as a fraction with a denominator of 100 or as a decimal.
For instance, 50% is equivalent to 50/100, which simplifies to 1/2, and also to 0.5 as a decimal. This fundamental understanding is key to solving percentage problems effectively.
Calculating "20 is What Percent of 15?"
Now, let's address the core question: "20 is what percent of 15?" This translates into a mathematical equation:
x% of 15 = 20
Where 'x' represents the unknown percentage we need to find. To solve for 'x', we can follow these steps:
-
Rewrite the equation: First, we rewrite the equation using the fractional representation of a percentage:
(x/100) * 15 = 20
-
Isolate 'x': Our goal is to isolate 'x' to find its value. We can start by multiplying both sides of the equation by 100:
x * 15 = 20 * 100
This simplifies to:
15x = 2000
-
Solve for 'x': Now, we divide both sides of the equation by 15 to solve for 'x':
x = 2000 / 15
x ≈ 133.33
Therefore, 20 is approximately 133.33% of 15.
Understanding the Result: Percentages Greater Than 100%
It's important to note that percentages can be greater than 100%. This simply means that the first number (20 in this case) is larger than the second number (15). A percentage greater than 100% indicates that the first number represents a value exceeding the second number's total.
Alternative Method: Using Proportions
Another effective method to solve percentage problems involves using proportions. We can set up a proportion using the given information:
20/15 = x/100
This proportion states that the ratio of 20 to 15 is equal to the ratio of x (the unknown percentage) to 100. To solve this proportion, we can cross-multiply:
20 * 100 = 15 * x
2000 = 15x
x = 2000 / 15
x ≈ 133.33
This method confirms our previous result: 20 is approximately 133.33% of 15.
Real-World Applications: Illustrative Examples
The concept of percentages is ubiquitous in various real-world applications. Understanding how to calculate percentages is essential in numerous scenarios, including:
- Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns all involve percentage calculations. For example, if you invest $15 and it grows to $20, your return on investment is 133.33%.
- Business: Analyzing sales figures, market share, and growth rates often involves working with percentages. Understanding these percentages can be crucial in making sound business decisions. A business that increases its sales from 15 units to 20 units has experienced a growth of 133.33%.
- Science: Many scientific experiments and analyses involve data expressed as percentages. For example, calculating the percentage of a specific element in a compound or the percentage of a population exhibiting a certain trait.
- Everyday Life: Calculating tips in restaurants, figuring out sale discounts in stores, and understanding statistics presented in news reports all rely on understanding and applying percentage calculations.
Expanding Your Percentage Skills: Further Exploration
Mastering percentage calculations opens doors to more complex mathematical concepts. Here are some areas to explore further:
- Percentage Increase and Decrease: Understanding how to calculate percentage increases and decreases is crucial for many applications. For example, calculating the percentage change in price, population, or any other quantity over time.
- Compound Interest: Compound interest is a powerful concept that builds upon the understanding of percentages. It involves calculating interest not only on the principal amount but also on accumulated interest.
- Statistical Analysis: Percentages are fundamental in statistical analysis, forming the basis of various measures and calculations.
Conclusion: The Power of Percentage Understanding
The question, "20 is what percent of 15?" serves as a springboard to a broader understanding of percentage calculations. While the answer – approximately 133.33% – is relatively straightforward to obtain, the process of arriving at the solution and the ability to apply this knowledge across various contexts are far more significant. By mastering percentage calculations and appreciating their applications, you equip yourself with a valuable tool applicable across many academic, professional, and personal scenarios. This knowledge empowers you to analyze data more effectively, make better-informed decisions, and navigate the quantitative aspects of the world around you with increased confidence and accuracy. So, the next time you encounter a percentage problem, remember the fundamentals, embrace the process, and reap the rewards of this crucial mathematical skill.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 20 Is What Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.