20 Is What Percent Of 25
News Co
Apr 14, 2025 · 5 min read
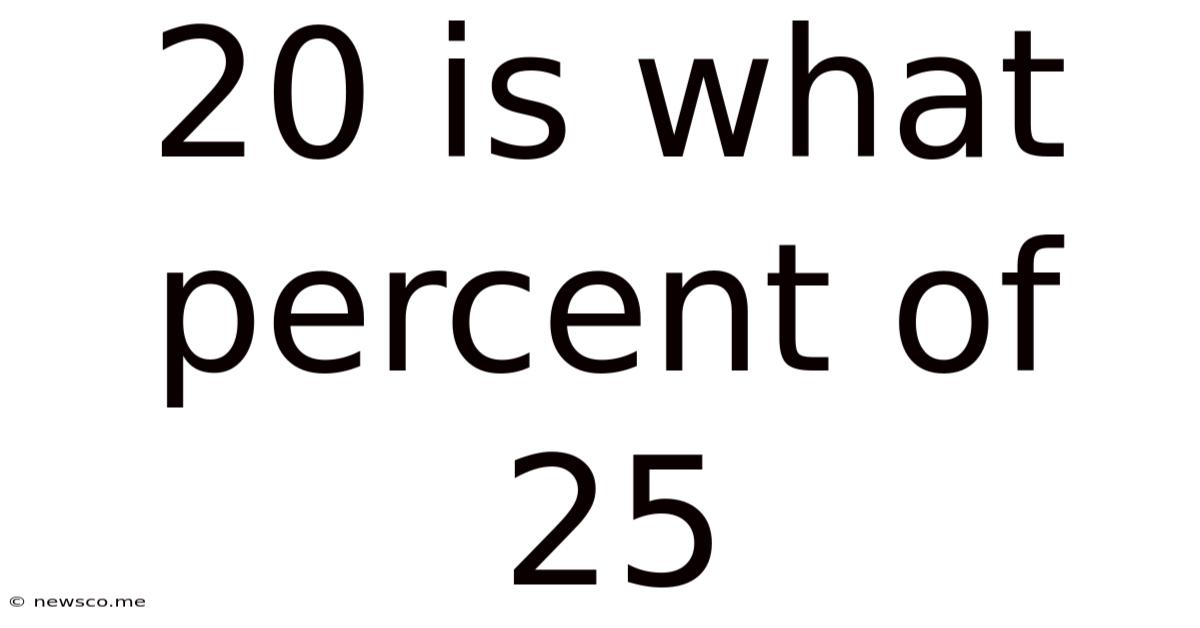
Table of Contents
20 is What Percent of 25? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "20 is what percent of 25?", unlocks a fundamental concept in mathematics with wide-ranging applications in everyday life. Understanding percentage calculations is crucial for various scenarios, from calculating discounts and sales tax to understanding financial reports and analyzing data. This article will delve deep into solving this specific problem, explaining the underlying principles, providing multiple solution methods, and exploring practical applications.
Understanding Percentages
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. Essentially, it represents a portion of a whole. For example, 50% means 50 out of 100, or one-half.
Method 1: Using the Formula
The most straightforward method to determine what percentage 20 represents of 25 is to use the basic percentage formula:
(Part / Whole) x 100 = Percentage
In our case:
- Part: 20
- Whole: 25
Substituting these values into the formula:
(20 / 25) x 100 = Percentage
This simplifies to:
0.8 x 100 = 80
Therefore, 20 is 80% of 25.
Method 2: Proportion Method
Another effective way to solve this problem is by setting up a proportion. A proportion demonstrates the equality of two ratios. We can set up the proportion as follows:
20/25 = x/100
Here, 'x' represents the unknown percentage we're trying to find. To solve for 'x', we cross-multiply:
20 * 100 = 25 * x
2000 = 25x
Now, divide both sides by 25:
x = 2000 / 25
x = 80
Again, we arrive at the answer: 20 is 80% of 25.
Method 3: Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
First, represent the problem as a fraction: 20/25
Next, simplify the fraction by dividing the numerator (20) by the denominator (25):
20 ÷ 25 = 0.8
Finally, multiply the decimal by 100 to convert it to a percentage:
0.8 x 100 = 80%
This confirms, once again, that 20 is 80% of 25.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world scenarios. Here are some examples:
-
Discounts and Sales: Retail stores frequently offer discounts expressed as percentages. For example, a 20% discount on a $100 item means you'll save $20 (20% of $100). Understanding percentage calculations allows you to quickly determine the final price after the discount is applied.
-
Taxes: Sales tax, income tax, and other taxes are usually calculated as a percentage of the purchase price or income. Knowing how to calculate percentages helps you determine the total amount you'll need to pay, including taxes.
-
Tips and Gratuities: When dining out or receiving services, it's customary to leave a tip, often expressed as a percentage of the bill. Calculating the tip amount accurately requires understanding percentage calculations.
-
Financial Analysis: Percentage changes are frequently used in financial analysis to track growth or decline in various metrics, such as profits, sales, or investments. For instance, comparing year-over-year sales growth requires calculating percentage changes.
-
Data Analysis: Percentages are extensively used to represent data in a more easily understandable and comparable format. For example, expressing survey results as percentages allows for clearer comparisons between different groups.
-
Grade Calculations: In education, grades are often expressed as percentages, reflecting the student's performance relative to the total possible score. Understanding percentages is critical for students to monitor their academic progress.
-
Ingredient Ratios in Recipes: Many recipes express ingredient amounts as percentages of the total weight or volume. This allows for scaling recipes up or down easily.
-
Statistical Analysis: Percentage calculations are a cornerstone of statistical analysis, used in everything from hypothesis testing to confidence intervals.
Expanding on the Concept: Finding the Whole or the Part
While our initial question focused on finding the percentage, the percentage formula can be rearranged to solve for the whole or the part if other values are known.
- Finding the Whole: If you know the percentage and the part, you can find the whole using this modified formula:
Whole = (Part / Percentage) * 100
- Finding the Part: If you know the percentage and the whole, you can find the part using this modified formula:
Part = (Percentage / 100) * Whole
Advanced Percentage Calculations: Compounding and More
Beyond basic percentage calculations, more complex scenarios involve compounding percentages or dealing with multiple percentages applied sequentially. These require a deeper understanding of mathematical principles but are crucial for advanced applications. For instance:
-
Compound Interest: Compound interest calculations involve repeatedly applying a percentage to a growing principal amount. This differs significantly from simple interest, where the interest is calculated only on the principal.
-
Percentage Increase/Decrease: Calculating the percentage increase or decrease between two values requires a slightly modified formula, taking into account the initial and final values.
-
Multiple Percentages: Applying multiple percentages sequentially, such as a discount followed by a sales tax, requires careful order of operations to ensure accurate calculations.
Conclusion
Determining that 20 is 80% of 25 is a foundational step in grasping the broader concept of percentages. This seemingly simple calculation reveals a powerful mathematical tool with far-reaching applications in daily life, finance, data analysis, and various other fields. Mastering percentage calculations equips you with a valuable skill set, empowering you to make informed decisions, interpret data effectively, and navigate numerous real-world scenarios with confidence. From understanding simple discounts to analyzing complex financial data, a firm grasp of percentages is invaluable. Remember to practice regularly to hone your skills and develop a deep understanding of this essential mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about 20 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.