20 Is What Percent Of 80
News Co
Apr 13, 2025 · 4 min read
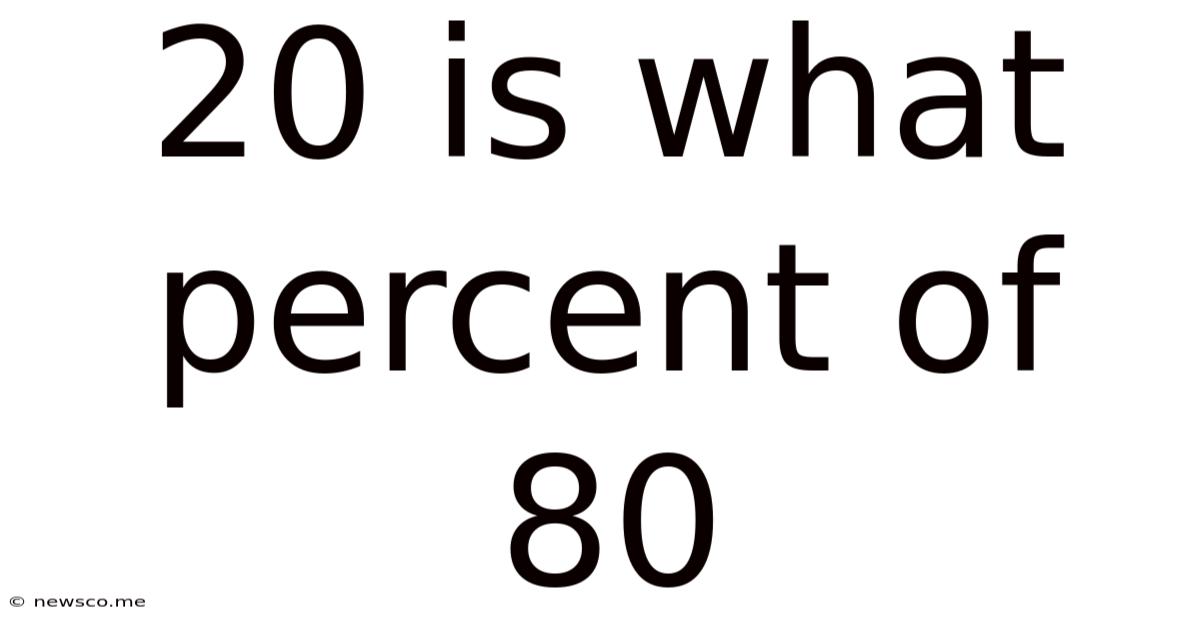
Table of Contents
20 is What Percent of 80? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This comprehensive guide will delve into the question, "20 is what percent of 80?", providing not only the answer but also a deep dive into the methodology, practical applications, and related percentage calculations. We'll explore different approaches, ensuring you grasp the core concepts and can confidently tackle similar percentage problems in the future.
Understanding the Basics of Percentages
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent" or "per hundred." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Key Terms and Concepts
- Percentage: A portion or fraction of a whole, expressed as a number out of 100.
- Whole: The total amount or value you're considering. In our example, 80 is the whole.
- Part: The portion of the whole you're interested in. In our example, 20 is the part.
Calculating "20 is What Percent of 80?"
There are several ways to calculate the percentage. Let's explore the most common methods:
Method 1: Using the Percentage Formula
The most straightforward method uses the basic percentage formula:
(Part / Whole) x 100% = Percentage
In our case:
(20 / 80) x 100% = Percentage
- Divide the part by the whole: 20 / 80 = 0.25
- Multiply the result by 100%: 0.25 x 100% = 25%
Therefore, 20 is 25% of 80.
Method 2: Using Proportions
We can also solve this using proportions. We set up a proportion where 'x' represents the unknown percentage:
20/80 = x/100
To solve for 'x', we cross-multiply:
20 * 100 = 80 * x
2000 = 80x
x = 2000 / 80
x = 25
Therefore, x = 25%, confirming our previous result.
Method 3: Simplifying the Fraction
Before multiplying by 100, we can simplify the fraction 20/80. Both numbers are divisible by 20:
20/80 = 1/4
Now, converting the simplified fraction to a percentage:
(1/4) x 100% = 25%
This method emphasizes the importance of simplifying fractions for easier calculations.
Practical Applications of Percentage Calculations
Understanding percentage calculations has numerous real-world applications:
1. Discounts and Sales
Retail stores frequently advertise discounts as percentages. For example, a 25% discount on a $100 item means you save $25 (25% of $100). This calculation helps determine the final price you'll pay.
2. Taxes and Interest
Taxes and interest are often expressed as percentages. Knowing how to calculate percentages helps you determine the exact amount of tax or interest you'll owe.
3. Financial Analysis
Percentage changes are crucial for tracking financial performance. For instance, comparing year-over-year revenue growth as a percentage helps assess the success of a business.
4. Data Analysis and Statistics
Percentages are extensively used in data analysis to represent proportions and trends. They simplify complex data into easily understandable formats.
5. Grade Calculations
In education, grades are frequently expressed as percentages, making it easy to compare student performance and track progress.
Variations and Related Percentage Problems
Let's explore some variations of the original problem and similar percentage calculations:
1. Finding the Whole
What if we knew the percentage and the part, and we needed to find the whole? For example:
25% of what number is 20?
We can use the formula:
(Part / Percentage) x 100 = Whole
(20 / 25) x 100 = 80
Therefore, 25% of 80 is 20.
2. Finding the Part
What if we knew the percentage and the whole, and we needed to find the part? For example:
What is 25% of 80?
We use the formula:
(Percentage / 100) x Whole = Part
(25 / 100) x 80 = 20
Therefore, 25% of 80 is 20.
3. Percentage Increase/Decrease
Calculating percentage increases or decreases involves finding the difference between two values and expressing it as a percentage of the original value. For instance, if a price increases from $80 to $100, the percentage increase is:
((100 - 80) / 80) x 100% = 25%
Mastering Percentage Calculations: Tips and Tricks
- Practice regularly: The more you practice percentage calculations, the more comfortable you'll become.
- Use different methods: Try different approaches to solving percentage problems to find the method that works best for you.
- Simplify fractions: Simplifying fractions before converting them to percentages can make calculations easier.
- Use a calculator: A calculator can be a valuable tool for complex percentage calculations.
- Understand the context: Always carefully consider the context of the problem to ensure you're using the correct formula and interpreting the results correctly.
Conclusion
Understanding how to calculate percentages is a valuable skill applicable in various everyday situations. This comprehensive guide has explored different methods to determine that 20 is 25% of 80, emphasizing the importance of mastering percentage calculations. By understanding the underlying concepts and practicing different approaches, you can confidently tackle any percentage problem and utilize this knowledge to improve your problem-solving skills in various fields. Remember to practice regularly and utilize the tips and tricks provided to enhance your proficiency. Mastering percentages empowers you to interpret data, make informed decisions, and navigate numerous real-world scenarios effectively.
Latest Posts
Related Post
Thank you for visiting our website which covers about 20 Is What Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.