20 Percent Of What Is 15
News Co
May 03, 2025 · 4 min read
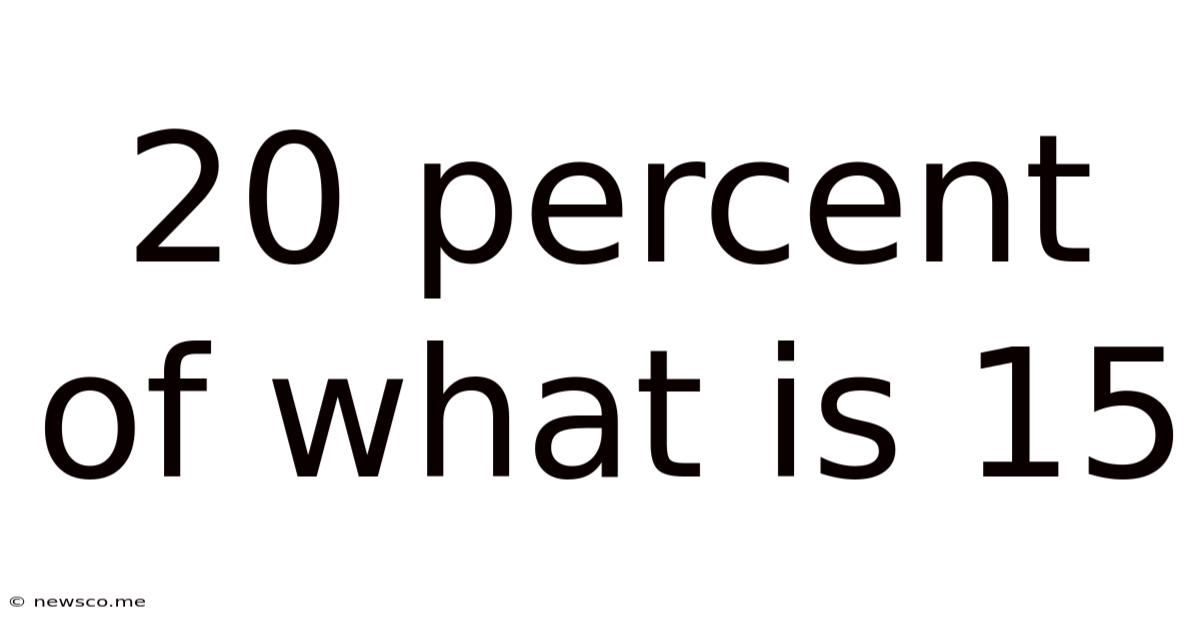
Table of Contents
20 Percent of What is 15? A Comprehensive Guide to Percentage Calculations
Finding 20% of a number is a fundamental concept in mathematics with widespread applications in daily life, from calculating discounts and sales tax to understanding financial statements and statistical data. This comprehensive guide will not only answer the question, "20 percent of what is 15?" but will also delve into the underlying principles of percentage calculations, explore various methods for solving such problems, and offer practical examples to solidify your understanding.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." For example, 20% means 20 out of 100, which can be written as the fraction 20/100 or the decimal 0.20. Understanding this fundamental concept is crucial for tackling percentage-based problems.
Key Concepts:
- Percentage: A ratio expressed as a fraction of 100.
- Part: The portion of the whole represented by the percentage.
- Whole: The total amount or quantity.
Solving "20 Percent of What is 15?"
Our core problem is to find the original number (the "whole") when we know that 20% of it equals 15. We can solve this using several methods:
Method 1: Using the Equation
This is the most direct approach. We can set up an equation to represent the problem:
0.20 * x = 15
Where 'x' represents the unknown whole number. To solve for 'x', we divide both sides of the equation by 0.20:
x = 15 / 0.20
x = 75
Therefore, 20% of 75 is 15.
Method 2: Using Proportions
Proportions offer a visual and intuitive way to solve percentage problems. We can set up a proportion:
20/100 = 15/x
This proportion states that the ratio of 20 to 100 is equal to the ratio of 15 to the unknown number (x). To solve for x, we cross-multiply:
20x = 1500
Then, divide both sides by 20:
x = 75
Again, we find that 20% of 75 is 15.
Method 3: Using the Percentage as a Decimal
We can directly convert the percentage to a decimal and then solve the equation. As mentioned earlier, 20% is equivalent to 0.20. The equation becomes:
0.20 * x = 15
Solving for x:
x = 15 / 0.20 = 75
This method reaffirms our answer: 20% of 75 is 15.
Practical Applications of Percentage Calculations
Understanding percentage calculations has far-reaching applications in numerous areas:
1. Retail and Sales:
- Discounts: Stores often advertise discounts as percentages (e.g., "20% off"). Knowing how to calculate percentages helps consumers determine the actual savings.
- Sales Tax: Sales tax is added to the price of goods and services, expressed as a percentage.
- Markup: Businesses use percentage markup to determine the selling price of products based on their cost.
2. Finance and Investments:
- Interest Rates: Interest on loans and savings accounts is usually expressed as a percentage.
- Investment Returns: Investment returns are commonly calculated as percentages.
- Financial Statements: Financial statements like income statements and balance sheets utilize percentages extensively to analyze financial performance.
3. Statistics and Data Analysis:
- Data Representation: Percentages are used to represent data proportions effectively in graphs and charts.
- Probability and Statistics: Percentage calculations are fundamental in probability and statistical analysis.
- Surveys and Polls: Results from surveys and polls are often presented as percentages.
4. Everyday Life:
- Tipping: Calculating tips in restaurants usually involves percentage calculations.
- Meal Sharing: Dividing expenses among friends fairly often requires percentage calculations.
- Recipe Scaling: Adjusting recipe quantities based on the number of servings involves percentages.
Advanced Percentage Calculations
Beyond basic percentage calculations, there are more complex scenarios:
1. Calculating Percentage Increase or Decrease:
This involves finding the percentage change between two numbers. The formula is:
[(New Value - Old Value) / Old Value] * 100%
For instance, if a price increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] * 100% = 20%
2. Finding the Original Value after a Percentage Change:
If you know the new value and the percentage change, you can find the original value. For example, if a price increased by 10% to $110, you can find the original price as follows:
Let x be the original price:
x + 0.10x = 110
1.10x = 110
x = 110 / 1.10 = $100
3. Compound Interest:
Compound interest is interest calculated on the principal amount plus accumulated interest from previous periods. This involves repeated percentage calculations over time, and the formula is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Conclusion
The ability to calculate percentages is a valuable skill applicable across various domains. Understanding the fundamental principles and mastering different solving methods, such as using equations, proportions, and decimal conversions, empowers you to tackle a wide range of percentage-related problems effectively. This guide has provided a comprehensive approach to solving percentage problems, including practical applications and more advanced scenarios, enabling you to confidently handle percentage calculations in your daily life, work, and studies. Remember that consistent practice is key to mastering this essential mathematical concept. By applying the techniques outlined here and continuing to practice, you'll become proficient in solving percentage problems with ease.
Latest Posts
Latest Posts
-
A Line Passes Through The Points
May 07, 2025
-
Power Of A Product Rule Examples
May 07, 2025
-
What Is The Difference Between A Rate And A Ratio
May 07, 2025
-
What Is The Value Of 5 2
May 07, 2025
-
19 As A Fraction In Simplest Form
May 07, 2025
Related Post
Thank you for visiting our website which covers about 20 Percent Of What Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.