20 Percent Of What Number Is 10
News Co
May 08, 2025 · 5 min read
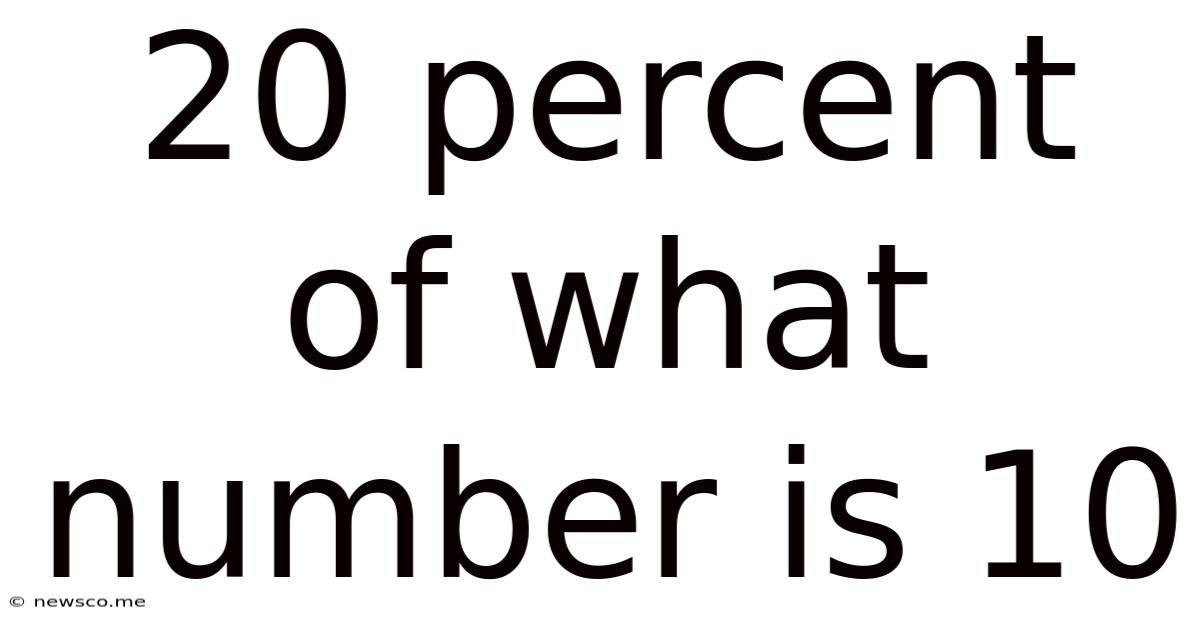
Table of Contents
20 Percent of What Number is 10? A Deep Dive into Percentage Calculations
Finding the answer to "20 percent of what number is 10?" might seem simple at first glance. However, understanding the underlying principles of percentage calculations is crucial, not just for solving this specific problem, but for tackling a wide range of mathematical challenges in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will walk you through several methods to solve this problem, explaining the concepts behind each approach and offering valuable insights into percentage calculations in general.
Understanding Percentages: The Foundation
Before diving into the solution, let's establish a solid understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 20% can be written as the fraction 20/100, or the decimal 0.20. This fundamental understanding is key to solving percentage problems efficiently.
Method 1: The Algebraic Approach
This method utilizes algebraic equations to solve for the unknown number. Let's represent the unknown number as 'x'. We can translate the problem "20 percent of what number is 10" into an algebraic equation:
0.20 * x = 10
To solve for 'x', we need to isolate it on one side of the equation. We can do this by dividing both sides of the equation by 0.20:
x = 10 / 0.20
x = 50
Therefore, 20% of 50 is 10. This algebraic approach offers a clear and structured method for solving percentage problems, particularly when dealing with more complex scenarios.
Method 2: The Proportion Method
This method leverages the concept of proportions to solve the problem. A proportion is a statement that equates two ratios. We can set up a proportion based on the given information:
20/100 = 10/x
This proportion states that the ratio of 20 to 100 is equal to the ratio of 10 to the unknown number 'x'. To solve for 'x', we can cross-multiply:
20 * x = 10 * 100
20x = 1000
Now, divide both sides by 20:
x = 1000 / 20
x = 50
Again, we arrive at the solution: 20% of 50 is 10. This method visually represents the relationship between the percentage and the whole number, making it an intuitive approach for some learners.
Method 3: The Reverse Percentage Method
This approach focuses on understanding that 20% represents a fraction of the whole. If 20% of a number is 10, then that means 20% is equivalent to 10. To find 100% (the whole number), we can set up a proportion:
20% / 100% = 10 / x
Simplifying the proportion:
1/5 = 10/x
Cross-multiplying:
x = 50
This confirms once again that 20% of 50 is 10. The reverse percentage method highlights the inverse relationship between the percentage and the whole, providing a different perspective on solving the problem.
Expanding on Percentage Calculations: Real-World Applications
Understanding how to solve "20 percent of what number is 10" provides a foundation for tackling numerous real-world scenarios. Let's explore some examples:
1. Sales and Discounts:
Imagine a store offering a 20% discount on an item, and the discount amount is $10. Using the methods discussed above, we can easily determine the original price of the item: $50. This type of calculation is crucial for both consumers and businesses.
2. Financial Analysis:
In finance, percentages are essential for understanding financial statements, such as profit margins, return on investment (ROI), and interest rates. Being able to quickly calculate percentages allows for better financial decision-making. For instance, if a company reports a 20% increase in profit, you can use these methods to calculate the actual profit increase.
3. Statistical Analysis:
Percentages are frequently used to represent data in statistical analysis. For example, if a survey reveals that 20% of respondents prefer a particular brand, understanding how to calculate the total number of respondents is necessary for drawing meaningful conclusions.
4. Everyday Calculations:
Percentage calculations are not limited to complex scenarios. They are frequently used in everyday life, such as calculating tips, splitting bills, or determining the amount of ingredients needed for a recipe based on a percentage increase or decrease.
Beyond the Basics: More Complex Percentage Problems
While the problem "20 percent of what number is 10" serves as an excellent introductory exercise, percentage calculations can become significantly more complex. Here are some examples of more challenging scenarios and how to approach them:
-
Compound Interest: Calculating compound interest involves repeated percentage calculations over time. This requires understanding exponential growth and is commonly used in banking and investment calculations.
-
Percentage Change: Determining the percentage increase or decrease between two values requires a different approach. The formula for percentage change is: [(New Value - Old Value) / Old Value] * 100%.
-
Percentage Points: It's important to differentiate between percentage points and percentages. A change from 20% to 30% is a 10 percentage point increase, but a 50% increase in the percentage itself. Understanding this distinction is critical for accurate interpretation of data.
-
Multiple Percentage Changes: Calculating the effect of multiple successive percentage increases or decreases requires careful consideration of the order of operations.
Mastering Percentage Calculations: Tips and Tricks
Here are some tips to help improve your percentage calculation skills:
-
Practice Regularly: The more you practice, the more comfortable you'll become with different approaches and problem-solving strategies.
-
Use a Calculator: While understanding the underlying principles is crucial, using a calculator can significantly speed up the process, particularly for complex problems.
-
Convert Percentages to Decimals or Fractions: Working with decimals or fractions can often simplify the calculations, making them easier to manage.
-
Check Your Work: Always double-check your calculations to ensure accuracy. A small mistake can lead to significant errors in the final result.
-
Visual Aids: Using diagrams or visual aids can help you better understand the relationships between percentages and whole numbers.
Conclusion: The Power of Percentage Understanding
Solving "20 percent of what number is 10" may appear trivial, but it underscores the importance of understanding the fundamentals of percentage calculations. From everyday budgeting to complex financial analysis, the ability to confidently tackle percentage problems is an invaluable skill. By mastering the different approaches discussed and practicing regularly, you'll build a strong foundation for handling a wide range of percentage-related challenges, both simple and complex. Remember to use the concepts outlined in this article as a stepping stone for tackling more complex percentage problems and expanding your mathematical skills. The ability to confidently calculate percentages is a versatile skill that will serve you well in many aspects of life.
Latest Posts
Latest Posts
-
1000 Milligrams Is Equal To How Many Grams
May 08, 2025
-
4 Divided By 2 3 As A Fraction
May 08, 2025
-
Name The Vertex Of Each Angle
May 08, 2025
-
What Is 25 Percent Off 60 Dollars
May 08, 2025
-
What Are The Coordinates Of Point B
May 08, 2025
Related Post
Thank you for visiting our website which covers about 20 Percent Of What Number Is 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.