20 Percent Out Of What Will Make 15
News Co
Mar 30, 2025 · 5 min read
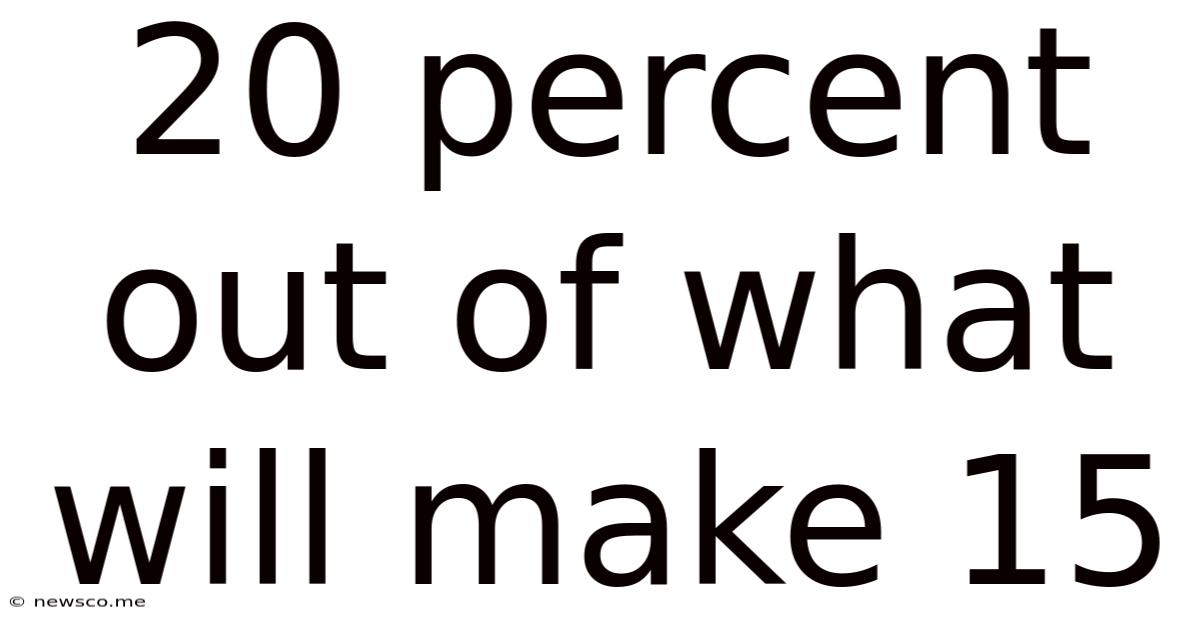
Table of Contents
Unlocking the Mystery: 20% of What Makes 15? A Deep Dive into Percentage Calculations
This seemingly simple question – "20% of what makes 15?" – can open up a fascinating world of percentage calculations and their practical applications. While the answer might seem readily apparent with a calculator, understanding the underlying process is crucial for various aspects of life, from budgeting and finance to sales and data analysis. This article will explore different methods to solve this problem, delve into the conceptual understanding of percentages, and examine real-world scenarios where this type of calculation proves invaluable.
Understanding Percentages: The Foundation
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of 100." For example, 20% can be written as 20/100, or its simplified fraction, 1/5. This means 20 parts out of every 100 parts.
Understanding this foundational concept is vital. It allows us to translate percentage problems into equations we can easily solve. This is the key to solving "20% of what makes 15?"
Method 1: The Algebraic Approach
This method involves setting up an algebraic equation and solving for the unknown. Let's represent the unknown number as 'x'. The problem can be translated into the following equation:
0.20 * x = 15
Here, 0.20 represents 20% (converted to decimal form by dividing by 100). To solve for x, we need to isolate it. We can do this by dividing both sides of the equation by 0.20:
x = 15 / 0.20
x = 75
Therefore, 20% of 75 makes 15. This algebraic approach is precise and highly effective, particularly when dealing with more complex percentage problems.
Method 2: The Ratio and Proportion Method
This method uses the concept of ratios and proportions to solve the problem. We can set up a proportion:
20/100 = 15/x
This proportion states that the ratio of 20 to 100 is equal to the ratio of 15 to the unknown number 'x'. To solve for 'x', we can cross-multiply:
20 * x = 15 * 100
20x = 1500
Dividing both sides by 20, we get:
x = 1500 / 20
x = 75
Again, we arrive at the same answer: 20% of 75 is 15. This method provides an alternative approach and reinforces the understanding of proportional relationships.
Method 3: The "Reverse Percentage" Method (Finding the Whole from a Part)
This method is particularly useful when dealing with scenarios where you know the percentage of a number and the resulting value, but you need to find the original number (the "whole"). We can visualize this as:
- Part = Percentage * Whole
In our case, we know the "part" (15) and the percentage (20%). We need to find the "whole". Rearranging the formula, we get:
- Whole = Part / Percentage
Substituting the values, we have:
- Whole = 15 / (20/100)
This simplifies to:
-
Whole = 15 / 0.20
-
Whole = 75
This approach directly addresses the problem's core—finding the original number from its 20% portion.
Real-World Applications: Where This Calculation Matters
The ability to solve problems like "20% of what makes 15?" is surprisingly relevant in many real-world scenarios:
1. Finance and Budgeting:
- Discounts: Imagine a store offering a 20% discount, and an item costs $15 after the discount. This calculation helps determine the original price.
- Sales Commissions: If a salesperson earns a 20% commission and received $15, you can calculate their total sales.
- Interest Calculations: Understanding percentage calculations is fundamental to comprehending interest rates on loans or investments.
2. Data Analysis and Statistics:
- Sample Sizes: In statistical analysis, determining the total population size based on a sample percentage is crucial.
- Percentage Change: Calculating percentage increases or decreases is essential for analyzing trends and patterns in data.
3. Business and Sales:
- Profit Margins: Understanding percentage profit margins is critical for businesses to assess their profitability.
- Market Share: Calculating market share percentages helps businesses understand their position relative to competitors.
4. Everyday Life:
- Tip Calculations: Determining the original bill amount when you know the tip percentage and amount.
- Recipe Scaling: Adjusting recipe ingredients based on a percentage increase or decrease.
Beyond the Basics: Expanding Your Percentage Skills
Mastering basic percentage calculations opens doors to more complex concepts:
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest.
- Percentage Points vs. Percentages: Understanding the distinction between these two terms is vital for accurate interpretation of data.
- Percentage Increase/Decrease: Calculating the percentage change between two values is crucial for analyzing trends.
Practical Exercises: Sharpening Your Skills
To solidify your understanding, try solving these problems:
- 15% of what makes 9?
- 30% of what makes 21?
- If a product costs $25 after a 10% discount, what was the original price?
- A salesperson earns a 5% commission on sales. If they earned $50, how much did they sell?
By practicing these exercises, you'll build confidence and fluency in solving percentage problems.
Conclusion: The Power of Percentage Understanding
The simple question, "20% of what makes 15?" might appear trivial at first glance. However, exploring its solution through different methods reveals the underlying principles of percentage calculations and their profound impact across various aspects of our lives. Mastering these principles empowers you to navigate financial decisions, analyze data effectively, and solve everyday problems with greater confidence and accuracy. Remember that practice is key; the more you work with percentages, the more comfortable and proficient you will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about 20 Percent Out Of What Will Make 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.