23 7 As A Mixed Number
News Co
Mar 17, 2025 · 5 min read
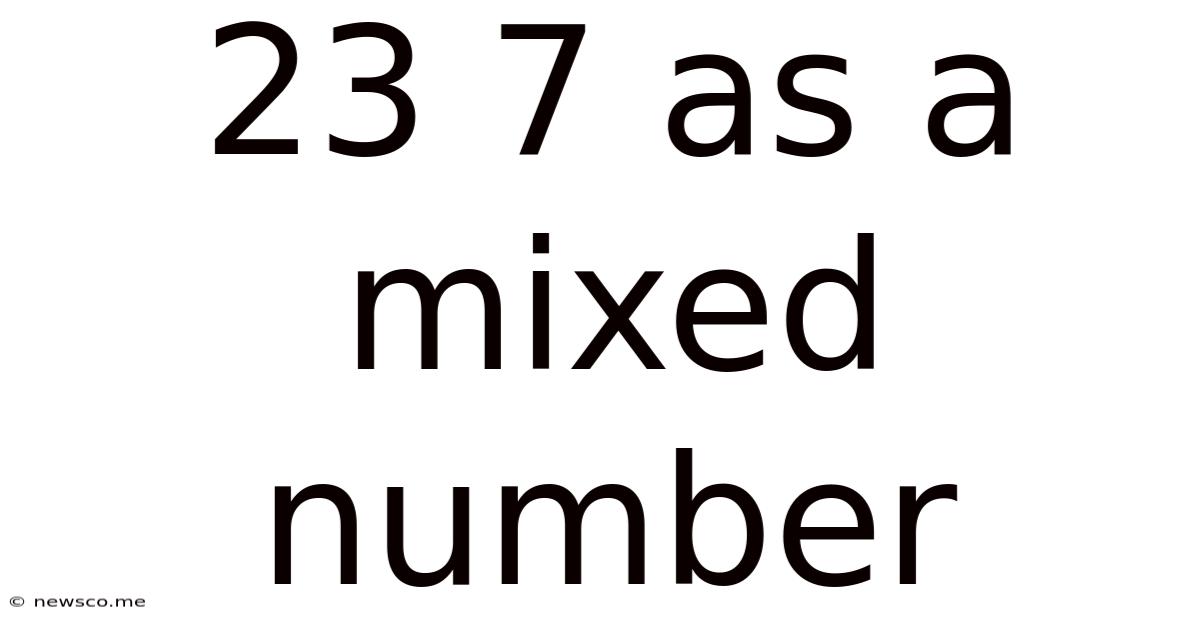
Table of Contents
23/7 as a Mixed Number: A Comprehensive Guide
Converting improper fractions to mixed numbers is a fundamental skill in arithmetic. This comprehensive guide will delve deep into the process of transforming the improper fraction 23/7 into its mixed number equivalent, exploring various methods and providing ample examples to solidify your understanding. We'll also explore the broader context of fractions and mixed numbers, their applications, and how to perform related operations.
Understanding Improper Fractions and Mixed Numbers
Before we dive into converting 23/7, let's establish a clear understanding of the terms involved.
-
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). For example, 23/7 is an improper fraction because 23 (numerator) is greater than 7 (denominator).
-
Mixed Number: A mixed number is a combination of a whole number and a proper fraction. A proper fraction is a fraction where the numerator is less than the denominator. For example, 3 2/7 is a mixed number; it represents three whole units and two-sevenths of another unit.
The core concept behind converting an improper fraction to a mixed number is to determine how many times the denominator goes into the numerator, representing the whole number part, and then expressing the remainder as a fraction.
Method 1: Long Division
The most straightforward method for converting 23/7 to a mixed number involves long division.
-
Divide the numerator by the denominator: Divide 23 by 7.
3 7|23 21 -- 2 -
Identify the quotient and remainder: The quotient (the result of the division) is 3, and the remainder is 2.
-
Express as a mixed number: The quotient becomes the whole number part, and the remainder becomes the numerator of the fraction, while the denominator remains the same. Therefore, 23/7 is equal to 3 2/7.
Method 2: Repeated Subtraction
This method is conceptually simpler, particularly for those who find long division challenging.
-
Repeatedly subtract the denominator from the numerator: Subtract 7 from 23 repeatedly until the result is less than 7.
23 - 7 = 16 16 - 7 = 9 9 - 7 = 2
-
Count the number of subtractions: You subtracted 7 three times. This becomes the whole number part of your mixed number.
-
Express the remainder as a fraction: The final result of the subtractions (2) is the remainder, which becomes the numerator of the fraction. The denominator remains 7.
-
Combine to form the mixed number: This gives us the same result: 3 2/7.
Visual Representation
Imagine you have 23 identical items, and you want to group them into sets of 7. You can form three complete sets of 7, with 2 items remaining. This visually represents the mixed number 3 2/7.
Applications of Improper Fractions and Mixed Numbers
Improper fractions and mixed numbers are essential in various real-world applications:
-
Cooking and Baking: Recipes often require fractional measurements, and converting between improper fractions and mixed numbers ensures accurate ingredient proportions. For example, a recipe might call for 23/7 cups of flour, which is easier to measure as 3 2/7 cups.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Converting between fractions helps ensure accuracy in calculations and project planning.
-
Data Analysis: Representing data as fractions and mixed numbers can provide a clearer understanding of proportions and ratios.
-
Everyday Life: Many everyday scenarios involve fractions, from sharing items equally to calculating distances or time.
Working with Mixed Numbers: Addition and Subtraction
Once you've converted an improper fraction to a mixed number, you can use it in further calculations. Let's explore addition and subtraction with mixed numbers, using our example of 3 2/7.
Addition:
To add mixed numbers, you add the whole numbers separately and the fractions separately. If the fractions have different denominators, you'll need to find a common denominator before adding.
Example: Add 3 2/7 + 1 3/7
- Add the whole numbers: 3 + 1 = 4
- Add the fractions: 2/7 + 3/7 = 5/7
- Combine the results: 4 5/7
Subtraction:
Subtracting mixed numbers is similar, but you might need to borrow from the whole number if the fraction in the minuend (the number being subtracted from) is smaller than the fraction in the subtrahend (the number being subtracted).
Example: Subtract 3 2/7 - 1 4/7
- Since 2/7 < 4/7, we borrow 1 from the whole number 3, converting it to 7/7.
- This gives us (2 + 7/7) 2/7 = 2 9/7
- Now subtract the whole numbers: 2 - 1 = 1
- Subtract the fractions: 9/7 - 4/7 = 5/7
- Combine the results: 1 5/7
Working with Mixed Numbers: Multiplication and Division
Multiplication and division with mixed numbers involve a slightly more complex process. Generally, it's easiest to convert mixed numbers into improper fractions before performing these operations.
Multiplication:
To multiply mixed numbers, convert them to improper fractions first, then multiply the numerators and the denominators. Finally, simplify the result and convert back to a mixed number if needed.
Example: Multiply 3 2/7 * 2
- Convert 3 2/7 to an improper fraction: (3 * 7 + 2) / 7 = 23/7
- Multiply by 2: (23/7) * (2/1) = 46/7
- Convert 46/7 to a mixed number: 6 4/7
Division:
To divide mixed numbers, convert them to improper fractions, then invert the second fraction (the divisor) and multiply.
Example: Divide 3 2/7 by 2
- Convert 3 2/7 to an improper fraction: 23/7
- Invert the divisor (2/1 becomes 1/2)
- Multiply: (23/7) * (1/2) = 23/14
- Convert 23/14 to a mixed number: 1 9/14
Conclusion: Mastering Fractions and Mixed Numbers
Understanding how to convert improper fractions to mixed numbers, like 23/7 to 3 2/7, is a fundamental building block in mathematics. This process is applicable across various fields and everyday scenarios. By mastering the techniques outlined above – long division, repeated subtraction, and understanding the underlying concepts – you’ll be well-equipped to confidently handle fractions and mixed numbers in any context. Remember to practice regularly to solidify your understanding and improve your computational speed and accuracy. This will not only improve your mathematical skills but also enhance your problem-solving abilities across a broad range of applications.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 23 7 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.