24 Is 60 Percent Of What Number
News Co
Apr 12, 2025 · 4 min read
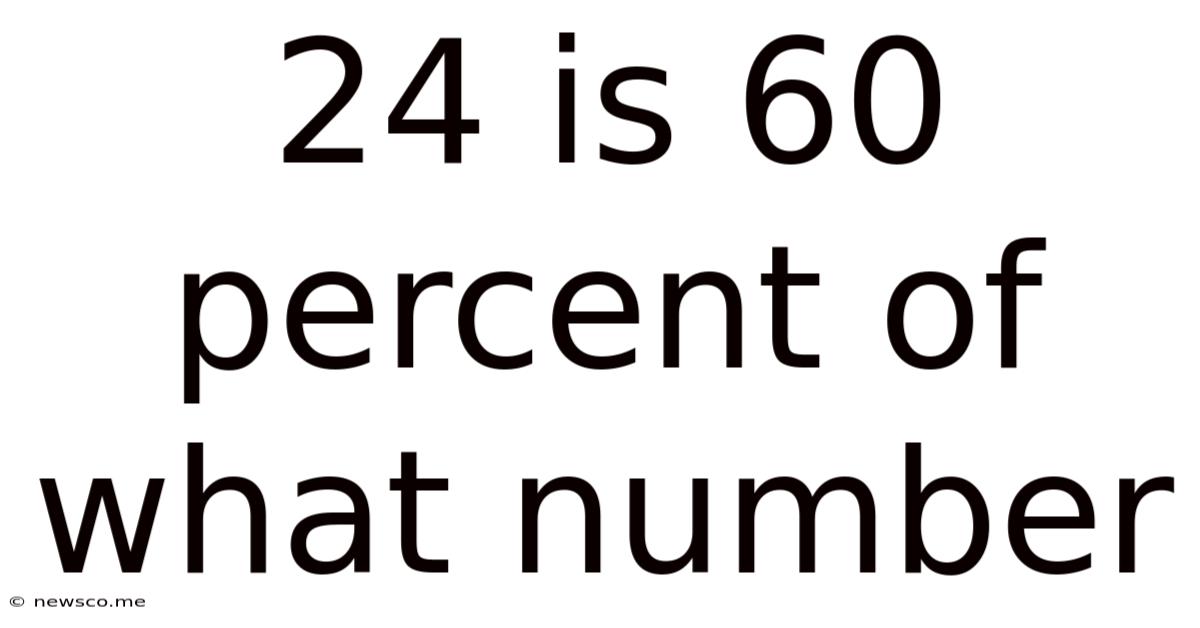
Table of Contents
24 is 60 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Percentage calculations are fundamental to many aspects of life, from calculating discounts and taxes to understanding financial reports and statistical data. This article delves deep into the question, "24 is 60 percent of what number?", providing a step-by-step solution, exploring different approaches, and demonstrating the broader application of percentage problems. We will also cover related concepts and provide you with practical examples to solidify your understanding.
Understanding Percentages
Before tackling the problem, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "percent" or "out of 100". For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Method 1: Using the Formula
The most straightforward way to solve "24 is 60 percent of what number?" is by using the percentage formula:
Part = Percent × Whole
In our problem:
- Part = 24 (this is the value representing 60% of the whole)
- Percent = 60% = 0.60 (we convert the percentage to a decimal by dividing by 100)
- Whole = x (this is the unknown number we need to find)
Substituting these values into the formula, we get:
24 = 0.60x
To solve for x, we divide both sides of the equation by 0.60:
x = 24 / 0.60
x = 40
Therefore, 24 is 60 percent of 40.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion shows the equality of two ratios. We can represent the problem as:
24/x = 60/100
This proportion states that the ratio of 24 to the unknown number (x) is equal to the ratio of 60 to 100 (60%). To solve this proportion, we cross-multiply:
24 * 100 = 60 * x
2400 = 60x
Now, divide both sides by 60:
x = 2400 / 60
x = 40
Again, we find that 24 is 60 percent of 40.
Method 3: Using the Concept of Unit Percentage
This method focuses on finding the value of 1% first and then scaling it up to find the whole.
If 60% of a number is 24, then 1% of that number would be:
24 / 60 = 0.4
Since 1% is 0.4, the whole number (100%) is:
0.4 * 100 = 40
This confirms that 24 is 60 percent of 40.
Practical Applications and Real-World Examples
Understanding percentage calculations is vital in various scenarios:
-
Sales and Discounts: If a store offers a 60% discount on an item, and the discounted price is $24, you can use this method to find the original price.
-
Tax Calculations: Determining the original price before taxes, given the tax rate and the final price.
-
Financial Analysis: Calculating profit margins, interest rates, and investment returns.
-
Scientific Research: Expressing experimental results and statistical data as percentages.
-
Everyday Life: Calculating tips, splitting bills, and understanding proportions in recipes.
Expanding the Concept: Solving for Different Variables
The fundamental principle demonstrated here applies to various percentage problems. You can adapt the methods shown above to solve for the percentage, the part, or the whole, depending on the information given. For example:
-
Finding the percentage: What percentage of 80 is 20?
-
Finding the part: What is 25% of 120?
-
Finding the whole: 15 is 30% of what number?
In each case, you can rearrange the formula (Part = Percent × Whole) or set up a proportion to find the unknown value.
Avoiding Common Mistakes
When working with percentages, common errors include:
-
Incorrect conversion of percentages to decimals: Remember to divide the percentage by 100 to get the decimal equivalent.
-
Mathematical errors: Double-check your calculations to avoid mistakes in addition, subtraction, multiplication, and division.
-
Misinterpreting the problem: Carefully read the problem statement to understand what is being asked for. Make sure you clearly identify the "part," "percent," and "whole" in each problem.
Advanced Percentage Problems and Concepts
While the example "24 is 60 percent of what number?" is relatively straightforward, percentage problems can become more complex. Here are some advanced concepts to explore:
-
Compound interest: Calculating interest on both the principal amount and accumulated interest.
-
Percentage change: Determining the increase or decrease in a quantity as a percentage.
-
Percentage points: The difference between two percentages. For example, a change from 10% to 15% is a five percentage point increase, not a 50% increase.
-
Working with multiple percentages: For example, calculating a final price after applying multiple discounts or taxes.
Mastering Percentage Calculations: Practice and Resources
Consistent practice is key to mastering percentage calculations. Start with simpler problems, gradually increasing the complexity as you gain confidence. Online resources, textbooks, and educational websites offer numerous practice problems and explanations.
Conclusion
The question, "24 is 60 percent of what number?", provides a fantastic entry point for understanding percentage calculations. By mastering the methods presented here—using the formula, setting up a proportion, or employing the unit percentage approach—you will develop a strong foundation for tackling a wide range of percentage problems in various academic and real-world contexts. Remember to practice regularly, pay close attention to details, and utilize available resources to refine your skills. With practice, you'll become proficient in solving even the most challenging percentage problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about 24 Is 60 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.