25 3 As A Mixed Number
News Co
Mar 20, 2025 · 5 min read
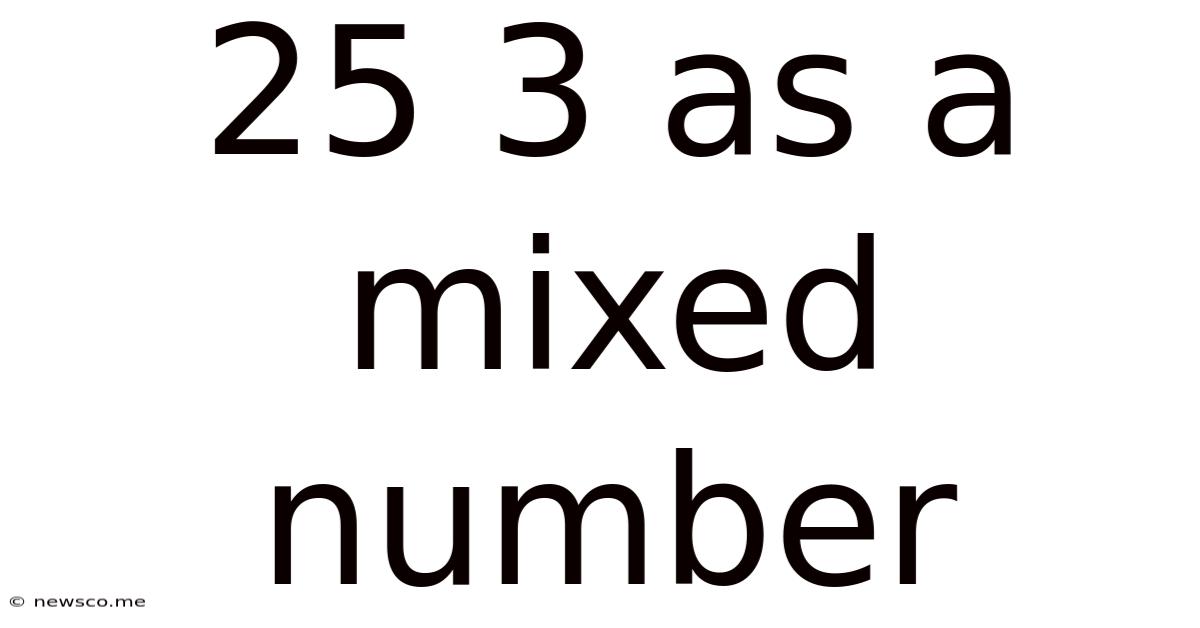
Table of Contents
25/3 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 25/3 into a mixed number, explaining the concept thoroughly and providing you with practical examples and tips. We'll explore different methods, address common misconceptions, and even touch upon the historical significance of fractions. By the end, you’ll not only know how to convert 25/3 but also possess a deeper understanding of fraction manipulation.
What is a Mixed Number?
Before we dive into converting 25/3, let's establish a clear understanding of what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1/2, 3/4, and 2/5 are all proper fractions. An improper fraction, on the other hand, has a numerator that is greater than or equal to the denominator. Examples include 5/4, 7/3, and 25/3 (our focus).
Converting 25/3 into a Mixed Number
The process of converting an improper fraction like 25/3 into a mixed number involves dividing the numerator by the denominator. Here's a step-by-step breakdown:
-
Divide the Numerator by the Denominator: Divide 25 by 3. This gives you a quotient (the result of the division) and a remainder.
25 ÷ 3 = 8 with a remainder of 1.
-
The Quotient Becomes the Whole Number: The quotient, 8, becomes the whole number part of your mixed number.
-
The Remainder Becomes the Numerator of the Fraction: The remainder, 1, becomes the numerator of the fractional part of your mixed number.
-
The Denominator Remains the Same: The denominator remains the same as in the original improper fraction (3).
Therefore, 25/3 as a mixed number is 8 1/3.
Understanding the Process: Visual Representation
Imagine you have 25 identical objects. If you want to group them into sets of 3, how many complete sets can you make? You can make 8 complete sets (8 x 3 = 24). You'll have 1 object left over. This leftover object represents the remainder. So you have 8 complete sets and 1/3 of a set remaining, giving you the mixed number 8 1/3. This visual representation helps solidify the understanding behind the mathematical process.
Alternative Methods for Conversion
While the long division method is the most common and widely understood, there are other approaches you can use to convert improper fractions to mixed numbers. These alternative methods can be helpful for mental calculations or when working with larger numbers:
-
Repeated Subtraction: Repeatedly subtract the denominator from the numerator until the result is less than the denominator. The number of times you subtracted is your whole number, and the remainder is your new numerator.
-
Using Multiplication and Estimation: Estimate how many times the denominator goes into the numerator. Multiply this estimate by the denominator and subtract the result from the numerator. The difference is the remainder.
While these methods are viable, the long division method remains the most straightforward and efficient for most scenarios.
Practical Applications of Mixed Numbers
Mixed numbers are prevalent in various real-life applications, making understanding their conversion essential. Here are a few examples:
-
Measurement: Imagine measuring the length of a piece of wood. You might measure it as 2 and 1/2 feet. This is a mixed number that represents a length greater than 2 feet but less than 3 feet.
-
Cooking: Recipes often involve mixed numbers. A recipe might call for 2 1/4 cups of flour.
-
Time: Expressing time frequently uses mixed numbers. For instance, you might say, "The race was 1 hour and 25 minutes long." This could be represented mathematically as 1 25/60 hours.
-
Data Analysis: Mixed numbers can appear in charts and graphs when dealing with quantities that fall between whole numbers.
Common Mistakes to Avoid
While the conversion process seems straightforward, certain errors can arise:
-
Incorrect Division: The most common mistake is an error in the division process. Double-check your division to ensure accuracy.
-
Misplacing the Remainder: Make sure the remainder becomes the numerator of the fraction and not the denominator.
-
Forgetting the Denominator: Remember that the denominator of the fractional part remains the same as the original improper fraction.
Careful attention to detail will help you avoid these pitfalls.
Expanding Your Knowledge: Further Exploration
This article has focused on converting 25/3 specifically, but the principles apply to any improper fraction. Practice with different improper fractions to solidify your understanding. You can create your own examples or find exercises online. Exploring additional fraction concepts, such as adding, subtracting, multiplying, and dividing fractions and mixed numbers, will further enhance your mathematical proficiency.
Understanding the historical context of fractions can also enrich your knowledge. Fractions have been used for thousands of years, evolving alongside mathematical advancements. Studying their history can provide a deeper appreciation for their significance in our modern world.
Beyond the Basics: Working with Larger Numbers
Converting larger improper fractions into mixed numbers follows the same principle: divide the numerator by the denominator. For instance, let's consider 175/12:
175 ÷ 12 = 14 with a remainder of 7.
Therefore, 175/12 as a mixed number is 14 7/12.
Conclusion: Mastering Fraction Conversions
Converting improper fractions to mixed numbers is a fundamental mathematical skill. This guide has provided a comprehensive understanding of the process, incorporating visual representations, alternative methods, practical applications, and common mistakes to avoid. By mastering this skill, you’ll be better equipped to handle various mathematical challenges in daily life and advanced studies. Remember to practice regularly and explore additional concepts related to fractions to enhance your understanding and become more confident in your mathematical abilities. Consistent practice is key to achieving proficiency in fraction manipulation and building a strong foundation in mathematics. Continuous learning and exploration will empower you to tackle more complex mathematical problems with ease and confidence.
Latest Posts
Related Post
Thank you for visiting our website which covers about 25 3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.