25 Is 20 Of What Number
News Co
Apr 18, 2025 · 5 min read
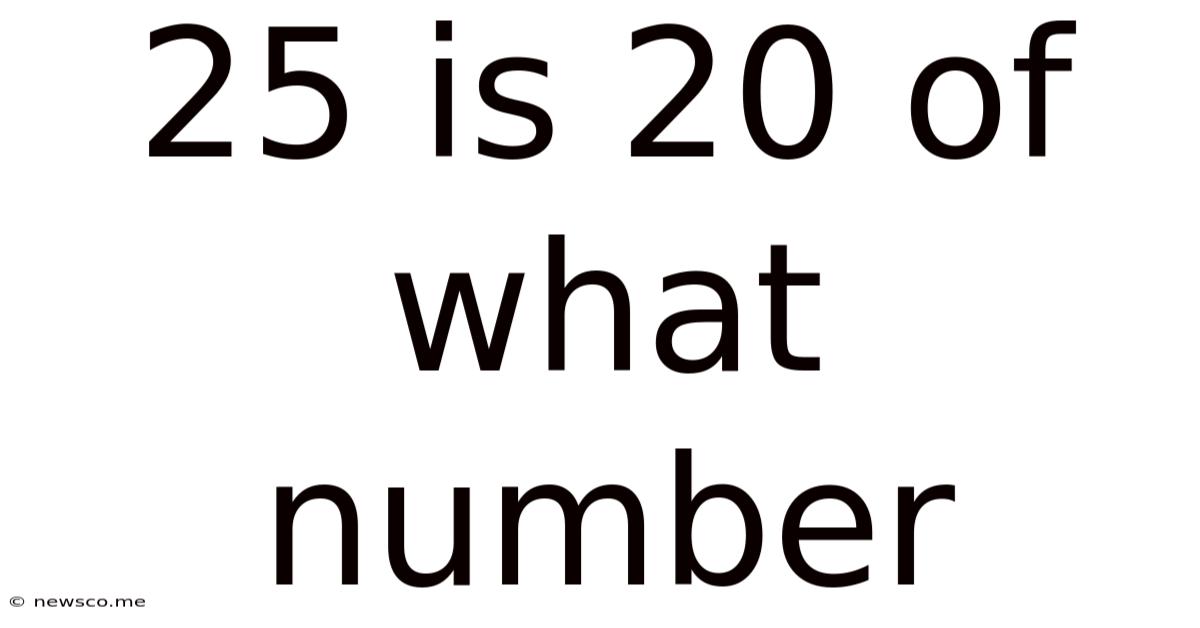
Table of Contents
25 is 20% of What Number? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "25 is 20% of what number?", opens the door to a world of percentage calculations crucial in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to solve this type of problem is a fundamental skill that empowers you to confidently tackle numerous real-world scenarios. This comprehensive guide will not only provide the solution but also delve into the underlying concepts, offering multiple approaches and practical applications.
Understanding Percentages
Before diving into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100." For instance, 20% can be written as the fraction 20/100 or the decimal 0.20. This representation forms the basis for all percentage calculations.
Key Percentage Concepts:
- Percentage: The portion of the whole, expressed as a fraction of 100.
- Part: The specific amount representing the percentage of the whole.
- Whole: The total amount from which the percentage is derived.
Solving "25 is 20% of What Number?"
Now, let's tackle the core question: "25 is 20% of what number?" We need to find the "whole" (the unknown number). We can solve this using several methods:
Method 1: Using the Equation
The most straightforward approach involves setting up an equation. Let's represent the unknown number as "x". The problem can be written as:
25 = 0.20 * x
To solve for x, we simply divide both sides of the equation by 0.20:
x = 25 / 0.20 = 125
Therefore, 25 is 20% of 125.
Method 2: Using Proportions
Another effective method utilizes proportions. We can set up a proportion as follows:
25/x = 20/100
This states that the ratio of the part (25) to the whole (x) is equal to the ratio of the percentage (20) to 100. To solve for x, we cross-multiply:
25 * 100 = 20 * x
2500 = 20x
x = 2500 / 20 = 125
Again, we find that x = 125.
Method 3: Using the Percentage Formula
The general percentage formula is:
Percentage = (Part / Whole) * 100
In our case, we know the percentage (20) and the part (25). We're solving for the whole:
20 = (25 / x) * 100
To solve for x, we can rearrange the equation:
x = (25 * 100) / 20 = 125
This confirms our previous results. 125 is the answer.
Real-World Applications of Percentage Calculations
Understanding how to solve percentage problems like "25 is 20% of what number?" has wide-ranging practical applications:
1. Finance and Budgeting:
- Calculating Savings: If you saved $25, representing 20% of your monthly income, you can easily determine your total monthly income ($125).
- Understanding Interest Rates: Calculating the principal amount based on accrued interest requires similar percentage calculations.
- Analyzing Investment Returns: Determining the initial investment amount based on a percentage return is another crucial application.
2. Retail and Sales:
- Calculating Original Prices: If an item is on sale for $25, representing 80% of the original price (20% discount), you can easily find the original price using percentage calculations.
- Determining Discount Percentages: Understanding the relationship between the discount amount and the original price allows for calculating the exact percentage discount.
- Profit Margin Analysis: Calculating profit margins based on sales and costs involves percentage computations.
3. Science and Research:
- Data Analysis: Many statistical analyses involve calculating percentages, proportions, and ratios.
- Experimental Results: Representing experimental results as percentages facilitates comparison and interpretation.
- Scientific Modeling: Percentage calculations are integral to numerous scientific models and simulations.
4. Everyday Life:
- Tip Calculation: Determining the pre-tip bill amount based on the tip percentage and tip amount.
- Recipe Scaling: Adjusting ingredient quantities in a recipe based on percentage increases or decreases.
- Survey Analysis: Representing responses in surveys as percentages for easy understanding.
Beyond the Basics: More Complex Percentage Problems
While the initial problem was relatively straightforward, percentage calculations can become more complex. Here are a few examples:
Example 1: Calculating Percentage Increase/Decrease
Let's say a product's price increased from $100 to $125. To find the percentage increase:
- Calculate the difference: $125 - $100 = $25
- Divide the difference by the original price: $25 / $100 = 0.25
- Multiply by 100 to express as a percentage: 0.25 * 100 = 25%
The price increased by 25%.
Example 2: Successive Percentage Changes
Imagine a 20% increase followed by a 10% decrease. These don't cancel each other out. Let's start with $100:
- 20% increase: $100 * 1.20 = $120
- 10% decrease on the new amount: $120 * 0.90 = $108
The final amount is $108, representing an overall increase of 8%.
Example 3: Percentage of a Percentage
Calculating a percentage of a percentage involves multiplying the percentages as decimals. For example, 20% of 50% is:
0.20 * 0.50 = 0.10 = 10%
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: Consistent practice is key to mastering percentage calculations. Work through various problems, starting with simple ones and gradually increasing complexity.
- Use Different Methods: Experiment with different approaches (equations, proportions, formula) to find the method that best suits your understanding.
- Utilize Online Resources: Numerous online calculators and tutorials are available to aid in your learning.
- Check Your Work: Always double-check your calculations to ensure accuracy.
- Real-world application: Try applying your knowledge to real-life situations - this will help you remember and understand the concepts better.
Conclusion
The seemingly simple question, "25 is 20% of what number?", unveils the importance of understanding percentage calculations. This skill is fundamental in various aspects of life, from personal finance to professional fields. By mastering different methods of solving percentage problems and consistently practicing, you'll develop a strong foundation in this essential mathematical skill, empowering you to confidently tackle numerous real-world challenges involving percentages. Remember to always check your work and utilize different methods to enhance your understanding and increase accuracy. The more you practice, the more proficient you'll become in handling any percentage-related problem you encounter.
Latest Posts
Related Post
Thank you for visiting our website which covers about 25 Is 20 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.