25 Is 50 Of What Number
News Co
May 02, 2025 · 5 min read
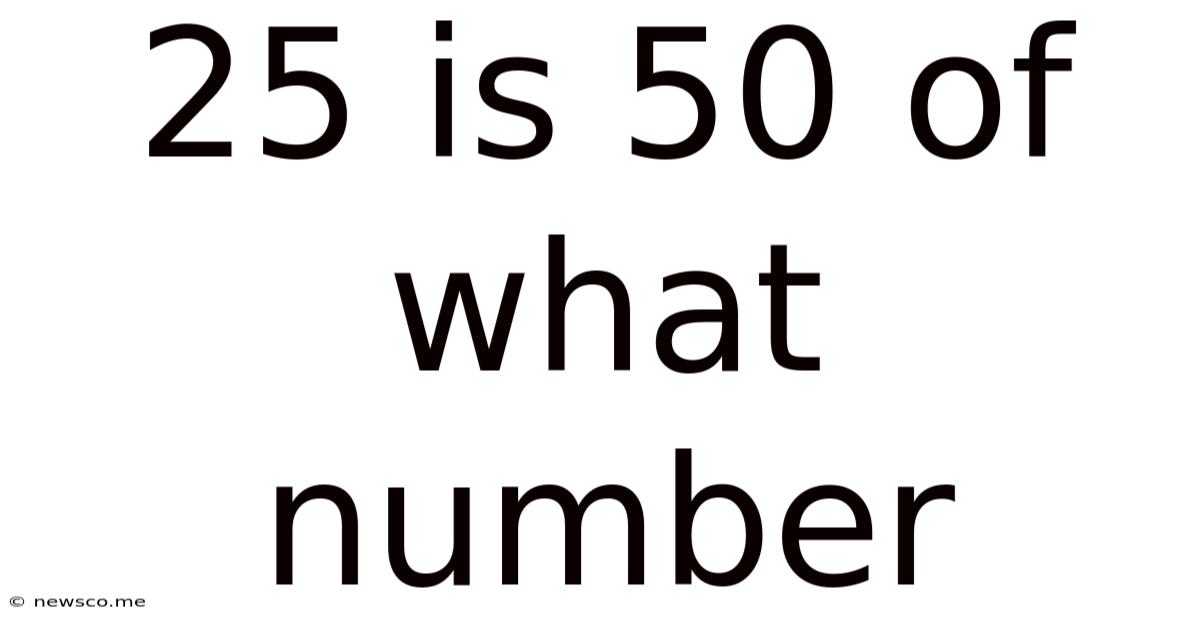
Table of Contents
25 is 50% of What Number? A Deep Dive into Percentage Calculations
Finding a percentage of a number is a fundamental mathematical skill with applications spanning various fields, from calculating discounts in retail to understanding financial reports. This article tackles the seemingly simple question, "25 is 50% of what number?" but delves far deeper than just providing the answer. We'll explore the underlying concepts, demonstrate multiple solution methods, and uncover the broader implications of percentage calculations.
Understanding Percentages: The Foundation
Before diving into the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100". For example, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5.
Understanding this fundamental relationship is crucial for tackling percentage problems. We often use percentages to represent proportions, ratios, or rates of change. They offer a standardized way to compare different quantities and easily visualize parts of a whole.
Method 1: Using the Percentage Formula
The most straightforward method to solve "25 is 50% of what number?" involves using the standard percentage formula:
Part = Percentage × Whole
In our problem:
- Part: 25 (the given value)
- Percentage: 50% (or 0.5 as a decimal)
- Whole: This is the unknown value we need to find (let's represent it with 'x')
Substituting these values into the formula gives us:
25 = 0.5 × x
To solve for 'x', we divide both sides of the equation by 0.5:
x = 25 / 0.5 = 50
Therefore, 25 is 50% of 50.
Method 2: Using Proportions
Another effective method leverages the concept of proportions. We can set up a proportion to represent the relationship between the given parts and the whole:
25/x = 50/100
This proportion states that the ratio of 25 to the unknown number (x) is equal to the ratio of 50 to 100 (which represents 50%). To solve for 'x', we can cross-multiply:
25 × 100 = 50 × x
2500 = 50x
Dividing both sides by 50:
x = 2500 / 50 = 50
Again, we arrive at the solution: 25 is 50% of 50.
Method 3: Thinking in Reverse Percentage
This method involves a more intuitive approach. If 25 represents 50% (or half) of a number, then the full number (100%) must be double the value of 25.
Therefore, 25 × 2 = 50
This method highlights the direct relationship between percentages and their corresponding fractions. Understanding these relationships can often lead to quicker solutions for simple percentage problems.
Expanding the Concept: Applications of Percentage Calculations
The ability to solve percentage problems like "25 is 50% of what number?" extends far beyond simple mathematical exercises. Here are some real-world applications:
1. Business and Finance:
- Profit margins: Calculating profit margins involves determining the percentage of revenue that represents profit. Understanding percentages helps businesses analyze their profitability and make informed decisions.
- Discounts and sales: Retailers frequently offer discounts expressed as percentages. Being able to quickly calculate the final price after a discount is essential for both consumers and businesses.
- Interest rates: Interest rates on loans and investments are always expressed as percentages. Calculating the total interest payable or the future value of an investment requires a solid understanding of percentage calculations.
- Tax calculations: Taxes are often calculated as a percentage of income or the value of goods and services. Accurate tax calculation relies on proficiency in percentage computations.
2. Science and Statistics:
- Data analysis: Percentages are frequently used to represent data proportions in scientific research and statistical analyses. They help researchers interpret trends, make comparisons, and draw meaningful conclusions.
- Probability and chance: Probability is often expressed as a percentage, indicating the likelihood of an event occurring. Understanding percentages helps in making informed decisions based on probabilistic outcomes.
3. Everyday Life:
- Tip calculations: Calculating a tip in a restaurant often involves finding a percentage of the total bill.
- Recipe scaling: Adjusting recipe quantities requires understanding percentages to maintain the correct ratios of ingredients.
- Understanding surveys and polls: Results from surveys and polls are commonly presented using percentages to summarize public opinion or preferences.
Beyond the Basics: More Complex Percentage Problems
While the problem "25 is 50% of what number?" is relatively straightforward, the principles involved extend to more complex scenarios. For instance:
- Finding the percentage increase or decrease: Calculating the percentage change between two values requires understanding how to express the difference as a percentage of the original value.
- Compound interest calculations: Compound interest involves calculating interest on both the principal amount and accumulated interest. This necessitates repeated percentage calculations.
- Working with multiple percentages: Problems involving multiple percentages, such as successive discounts or tax rates, require a stepwise approach and careful attention to detail.
Mastering Percentage Calculations: Tips and Practice
To truly master percentage calculations, consistent practice is key. Here are some tips to improve your proficiency:
- Start with the basics: Ensure you have a firm grasp of the fundamental concepts and formulas before tackling more complex problems.
- Practice regularly: Regular practice will build your confidence and speed in solving percentage problems.
- Use different methods: Experiment with various solution methods to find the approach that works best for you.
- Check your work: Always double-check your answers to ensure accuracy.
- Utilize online resources: Many online resources provide practice problems and tutorials on percentage calculations.
Conclusion: The Importance of Percentage Understanding
The seemingly simple question "25 is 50% of what number?" opens a door to a wide world of percentage applications. Mastering percentage calculations is not just a mathematical skill; it’s a crucial life skill with implications across various fields. By understanding the underlying principles and practicing consistently, you can confidently tackle percentage problems and utilize this powerful tool in your daily life and professional endeavors. Remember, the key is to understand the relationships between the parts and the whole, and to choose the method that best suits your problem-solving style. This comprehensive understanding will equip you to navigate the numerous percentage-based challenges that life presents.
Latest Posts
Related Post
Thank you for visiting our website which covers about 25 Is 50 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.