25 Is 80 Of What Number
News Co
May 08, 2025 · 4 min read
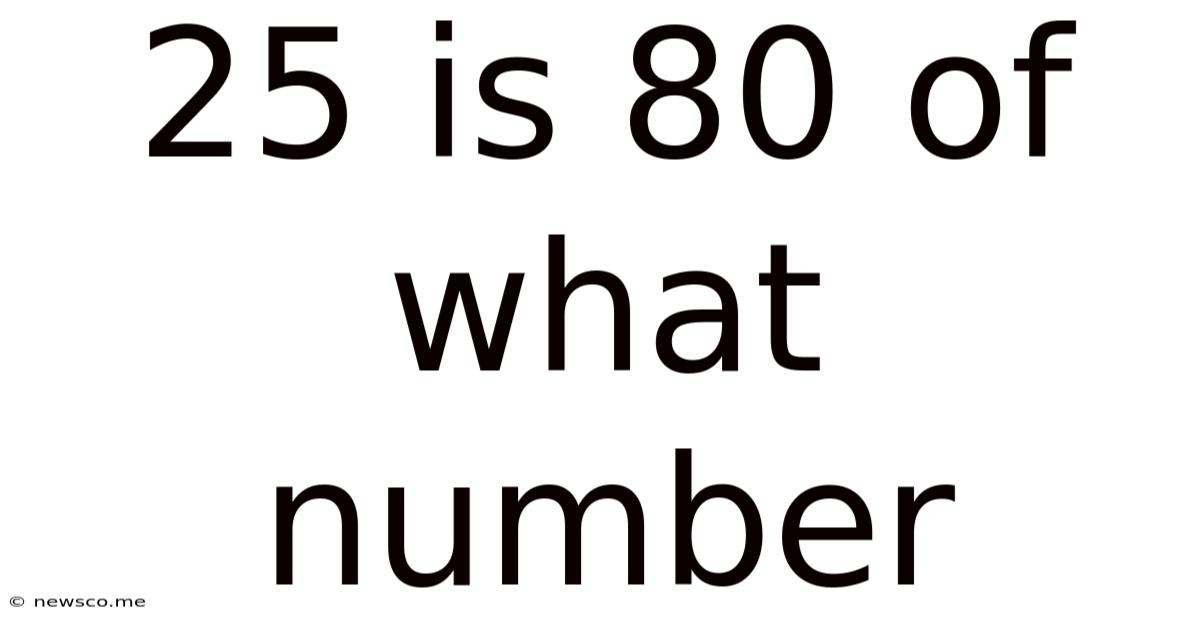
Table of Contents
25 is 80% of What Number? A Comprehensive Guide to Percentage Calculations
Finding an unknown number when you know a percentage of it is a common mathematical problem. This seemingly simple question – "25 is 80% of what number?" – actually opens the door to understanding fundamental concepts in percentage calculations and their applications in various real-world scenarios. This comprehensive guide will not only provide the solution but also delve into the underlying principles, offering multiple approaches to solving similar problems, and exploring practical examples to solidify your understanding.
Understanding Percentages
Before we dive into the solution, let's briefly review the concept of percentages. A percentage is a way of expressing a fraction or ratio as a part of 100. The symbol "%" signifies "per hundred." Therefore, 80% means 80 out of 100, or 80/100, which simplifies to 4/5.
Method 1: Using the Equation
The most straightforward method involves setting up an equation. Let's represent the unknown number as 'x'. We can translate the problem "25 is 80% of what number?" into the following equation:
25 = 0.80x
Here, we've converted 80% to its decimal equivalent (80/100 = 0.80). To solve for 'x', we simply divide both sides of the equation by 0.80:
x = 25 / 0.80
x = 31.25
Therefore, 25 is 80% of 31.25.
Method 2: Using Proportions
Another effective method utilizes proportions. We can set up a proportion where one ratio represents the known percentage and the other represents the unknown number:
25/x = 80/100
This proportion states that 25 is to x as 80 is to 100. To solve for x, we can cross-multiply:
25 * 100 = 80 * x
2500 = 80x
Now, divide both sides by 80:
x = 2500 / 80
x = 31.25
Again, we find that 25 is 80% of 31.25.
Method 3: Working Backwards from the Percentage
This method involves a slightly different approach. Since 25 represents 80% of the unknown number, we can find what 1% represents and then scale up to 100%.
First, we find the value of 1%:
25 / 80 = 0.3125
This means 1% of the unknown number is 0.3125. To find the whole number (100%), we multiply by 100:
0.3125 * 100 = 31.25
Therefore, the unknown number is 31.25.
Practical Applications
The ability to solve percentage problems like this has numerous real-world applications across various fields:
1. Finance and Business:
- Calculating Sales: If a store reports sales of $25,000 and this represents 80% of their projected sales, they can use this method to determine their projected total sales.
- Analyzing Profit Margins: Businesses use percentage calculations to understand their profit margins based on costs and revenue.
- Investment Returns: Calculating returns on investments often involves working with percentages and understanding the growth or loss relative to the initial investment.
2. Science and Statistics:
- Data Analysis: Scientists and statisticians frequently use percentages to express data proportions and relationships.
- Experimental Results: Percentage calculations are vital in interpreting experimental results and drawing conclusions.
3. Everyday Life:
- Discounts and Sales Tax: Calculating discounts in stores or adding sales tax to purchases involves percentage calculations.
- Tipping in Restaurants: Determining the appropriate tip amount often involves calculating a percentage of the total bill.
- Recipe Scaling: Adjusting recipe ingredient quantities proportionally involves percentage calculations.
Beyond the Basics: Handling Different Percentage Scenarios
While this example focuses on finding the "whole" from a known percentage, the underlying principles can be adapted to solve a variety of percentage-related problems. Here are some examples:
- Finding the percentage: If you know the whole number (31.25) and a part of it (25), you can easily calculate the percentage: (25/31.25) * 100 = 80%.
- Finding the part: If you know the whole number (31.25) and a percentage (say, 50%), you can find the part: 31.25 * 0.50 = 15.625.
- Percentage Increase/Decrease: Calculating percentage changes involves finding the difference between two values and then expressing that difference as a percentage of the original value. This is crucial for tracking growth or decline in various metrics.
Tips for Solving Percentage Problems
Here are some helpful tips to efficiently and accurately solve percentage problems:
- Convert percentages to decimals: This simplifies calculations and makes them easier to manage.
- Use consistent units: Ensure that all values are in the same units (e.g., dollars, kilograms, etc.) to avoid errors.
- Check your work: Always verify your calculations to ensure accuracy. You can often use an alternative method to cross-check your answer.
- Understand the context: Carefully read the problem statement to ensure you correctly identify the known and unknown quantities.
Conclusion: Mastering Percentage Calculations
Understanding percentage calculations is a valuable skill that has wide-ranging applications. The seemingly simple problem of "25 is 80% of what number?" provides a foundation for understanding more complex percentage-related problems. By mastering these techniques and employing the different approaches outlined in this guide, you'll be well-equipped to tackle various percentage-based challenges encountered in academics, professional life, and everyday scenarios. Remember that consistent practice and a clear understanding of the underlying principles are key to developing proficiency in percentage calculations.
Latest Posts
Related Post
Thank you for visiting our website which covers about 25 Is 80 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.