25 Is What Percent Of 100
News Co
Apr 12, 2025 · 4 min read
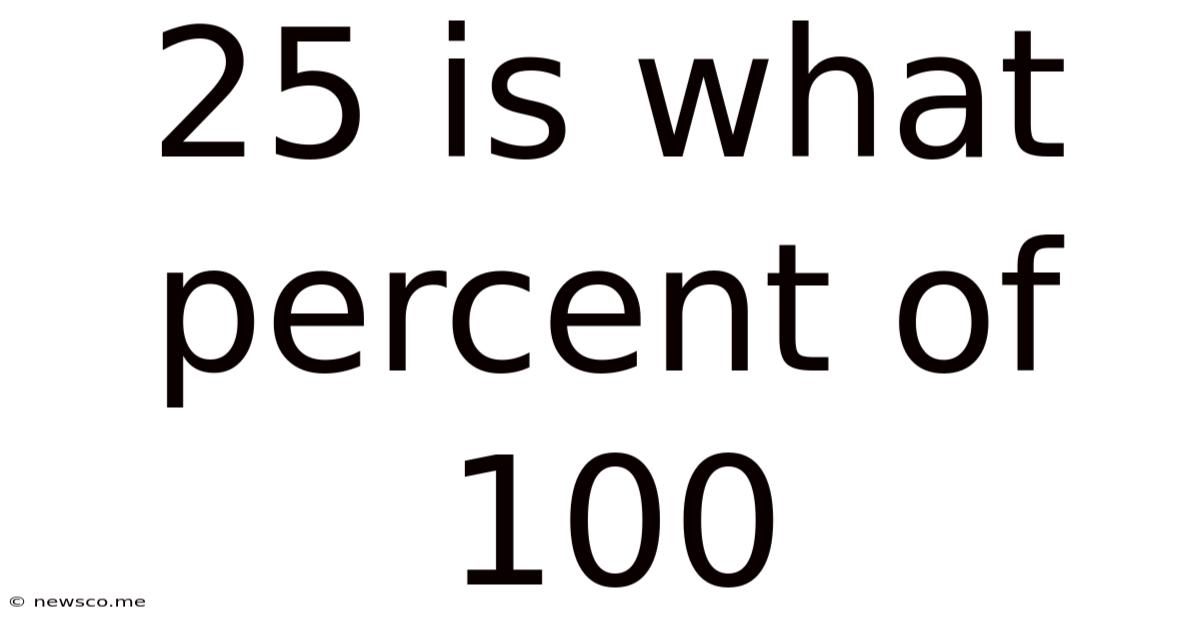
Table of Contents
25 is What Percent of 100: A Comprehensive Guide to Percentages
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will not only answer the question "25 is what percent of 100?" but also delve into the broader concept of percentages, providing you with the tools and knowledge to tackle similar problems with confidence.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "out of one hundred." Therefore, 25% means 25 out of 100, or 25/100.
Key Concepts:
- Percent Sign (%): This symbol is used to denote percentages.
- Numerator: The top number in a fraction (in this case, 25).
- Denominator: The bottom number in a fraction (in this case, 100).
Calculating Percentages: Different Methods
There are several ways to calculate percentages. Let's explore the most common methods, using the example of "25 is what percent of 100?".
Method 1: Using the Formula
The most straightforward method involves using a simple formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 25
- Whole: 100
Therefore:
(25 / 100) * 100 = 25%
So, 25 is 25% of 100.
Method 2: Understanding the Fraction
As mentioned earlier, a percentage is a fraction with a denominator of 100. Since we already have the fraction 25/100, we can directly convert it to a percentage:
25/100 = 25%
This method highlights the inherent relationship between fractions and percentages.
Method 3: Using Proportions
Proportions offer another effective way to solve percentage problems. We can set up a proportion:
25/100 = x/100
Where 'x' represents the percentage we're trying to find. Solving for 'x':
x = (25/100) * 100 = 25
Therefore, x = 25%, confirming our previous calculations.
Beyond the Basics: Solving More Complex Percentage Problems
While the example "25 is what percent of 100?" is straightforward, understanding the underlying principles allows you to tackle more complex problems. Let's explore some variations:
Finding the Percentage of a Number
What is 15% of 50?
Using the formula: (15/100) * 50 = 7.5
Therefore, 15% of 50 is 7.5.
Finding the Whole Number When Given a Percentage and Part
If 20% of a number is 10, what is the number?
We can set up a proportion:
20/100 = 10/x
Solving for x:
x = (10 * 100) / 20 = 50
Therefore, the number is 50.
Percentage Increase and Decrease
Percentage increase and decrease are common applications of percentages. For example:
-
Increase: A price increases from $50 to $60. The percentage increase is calculated as: ((60-50)/50) * 100 = 20%.
-
Decrease: A price decreases from $100 to $80. The percentage decrease is calculated as: ((100-80)/100) * 100 = 20%.
Real-World Applications of Percentages
Percentages are ubiquitous in everyday life. Here are some examples:
- Finance: Calculating interest rates, discounts, taxes, and profit margins.
- Retail: Determining sale prices and discounts.
- Science: Expressing experimental results and statistical data.
- Education: Calculating grades and test scores.
- Data Analysis: Representing proportions and trends in data sets.
Tips for Mastering Percentages
- Practice regularly: The more you practice, the more comfortable you'll become with percentage calculations.
- Use visual aids: Diagrams and charts can help visualize percentage relationships.
- Understand the underlying concepts: Focus on the meaning of percentages and their relationship to fractions and decimals.
- Break down complex problems: Divide complex problems into smaller, more manageable steps.
- Utilize online resources: Many online calculators and tutorials can help you practice and improve your understanding.
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate percentages?
A: The simplest method is using the formula: (Part / Whole) * 100 = Percentage.
Q: How do I convert a decimal to a percentage?
A: Multiply the decimal by 100 and add the percent sign (%). For example, 0.25 * 100 = 25%.
Q: How do I convert a fraction to a percentage?
A: Divide the numerator by the denominator, then multiply by 100 and add the percent sign (%). For example, 1/4 = 0.25 * 100 = 25%.
Q: What are some common percentage mistakes to avoid?
A: Common mistakes include incorrect placement of the decimal point, misunderstanding the terms "part" and "whole," and using the wrong formula.
Conclusion: Mastering the Art of Percentages
Understanding percentages is an essential life skill. By mastering the fundamental concepts and techniques outlined in this guide, you'll be equipped to confidently tackle various percentage problems in various contexts. Remember to practice regularly and utilize different methods to solidify your understanding. The ability to calculate and interpret percentages will undoubtedly enhance your problem-solving skills and improve your comprehension of numerical data in numerous fields. From financial literacy to data analysis, the ability to work with percentages is a valuable asset in navigating the complexities of the modern world.
Latest Posts
Related Post
Thank you for visiting our website which covers about 25 Is What Percent Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.