25 Is What Percent Of 200
News Co
May 04, 2025 · 5 min read
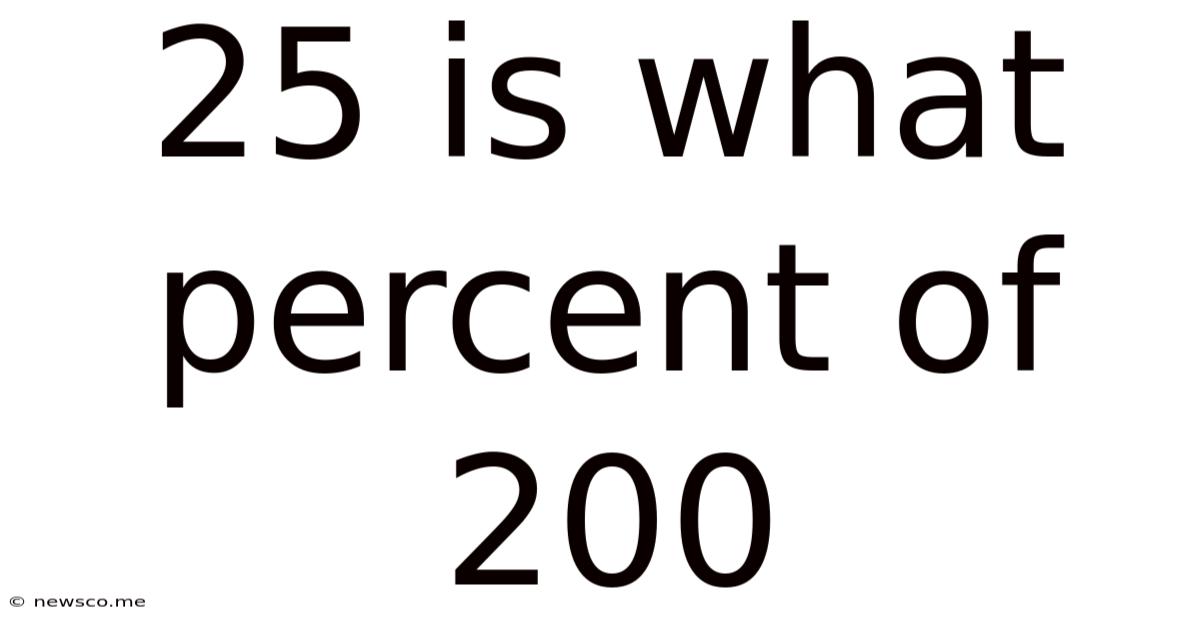
Table of Contents
25 is What Percent of 200? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This comprehensive guide will delve into the question, "25 is what percent of 200?", providing not only the answer but also a thorough explanation of the methodology, different approaches to solving the problem, and practical applications of percentage calculations.
Understanding Percentages: The Basics
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Key Concepts in Percentage Calculations:
- Part: This represents the value we're interested in expressing as a percentage of the whole. In our problem, 25 is the part.
- Whole: This is the total value to which the part is being compared. In our problem, 200 is the whole.
- Percentage: This is the value representing the part as a proportion of the whole, expressed as a percentage (%).
Calculating "25 is What Percent of 200?"
There are several ways to solve this percentage problem. Let's explore the most common and straightforward methods:
Method 1: Using the Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
Let's apply this to our problem:
(25 / 200) * 100 = Percentage
- Divide the part by the whole: 25 / 200 = 0.125
- Multiply the result by 100: 0.125 * 100 = 12.5
Therefore, 25 is 12.5% of 200.
Method 2: Using Proportions
Another effective approach involves setting up a proportion:
25/200 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
25 * 100 = 200 * x
2500 = 200x
x = 2500 / 200
x = 12.5
Again, we find that 25 is 12.5% of 200.
Method 3: Using Decimal Conversion
This method involves first converting the percentage to a decimal and then performing the calculation. Since we're looking for the percentage, we can set up the equation as follows:
Let x be the percentage.
Then, (x/100) * 200 = 25
Solving for x:
2x = 25
x = 12.5
Therefore, 25 is 12.5% of 200.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios. Here are some examples:
1. Retail Discounts:
Imagine a shirt originally priced at $200 is on sale for $25 off. Using the methods above, we can easily determine that the discount is 12.5%. This helps consumers understand the savings they're receiving.
2. Financial Analysis:
In finance, percentages are used extensively. For example, calculating interest rates, investment returns, and profit margins all rely on percentage calculations. A company might calculate its profit margin by comparing its profit (25) to its revenue (200) to find that its profit margin is 12.5%.
3. Data Analysis and Statistics:
Percentages are essential tools in interpreting statistical data. For example, if 25 out of 200 survey respondents answered "yes" to a particular question, the percentage of "yes" responses would be 12.5%. This allows for easy comparison and visualization of data.
4. Grade Calculation:
Many academic systems use percentages to represent grades. If a student scores 25 out of 200 possible points on a test, their score is 12.5%. This provides a standardized way to assess student performance.
Expanding on Percentage Calculations: More Complex Scenarios
While the example of "25 is what percent of 200?" provides a basic understanding, let's consider more complex scenarios to enhance your skills:
Scenario 1: Finding the Whole
Let's say we know that 15% of a number is 75. How do we find the original number (the whole)?
We can set up the equation:
(15/100) * x = 75
Solving for x:
0.15x = 75
x = 75 / 0.15
x = 500
Therefore, the whole number is 500.
Scenario 2: Finding the Part
If we know that 30% of a number is 60, what is the value of the part representing 30%? We can solve this using:
(30/100) * x = 60
0.3x = 60
x = 60 / 0.3
x = 200
The whole is 200, and the part representing 30% is 60.
Scenario 3: Percentage Increase/Decrease
Suppose a value increases from 200 to 225. To calculate the percentage increase:
- Find the difference: 225 - 200 = 25
- Divide the difference by the original value: 25 / 200 = 0.125
- Multiply by 100 to express as a percentage: 0.125 * 100 = 12.5%
Therefore, there's a 12.5% increase. Percentage decrease calculations follow a similar process.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The more you practice, the more comfortable and proficient you'll become.
- Understand the Formula: Memorize the basic percentage formula and apply it consistently.
- Use Different Methods: Try various methods (formula, proportion, decimal conversion) to find the approach that best suits your understanding.
- Check Your Work: Always double-check your calculations to ensure accuracy.
- Utilize Online Calculators: While understanding the underlying principles is crucial, online calculators can be helpful for verifying your answers or solving complex problems.
- Break Down Complex Problems: Decompose complex percentage problems into smaller, manageable steps.
By mastering percentage calculations, you'll enhance your problem-solving skills and improve your ability to analyze information across diverse fields. The seemingly simple question, "25 is what percent of 200?" serves as a gateway to a broader understanding of this essential mathematical concept. Remember to practice regularly and apply these techniques to real-world scenarios to solidify your knowledge.
Latest Posts
Latest Posts
-
What Is The Volume Of The Cone Below Apex
May 05, 2025
-
How To Find The Perimeter Of A Polygon With Vertices
May 05, 2025
-
Convert 45 Degrees F To Celsius
May 05, 2025
-
Do All Quadrilaterals Have Right Angles
May 05, 2025
-
Find The Exact Values Of The Six Trigonometric Functions
May 05, 2025
Related Post
Thank you for visiting our website which covers about 25 Is What Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.