25 Is What Percentage Of 40
News Co
Mar 20, 2025 · 4 min read
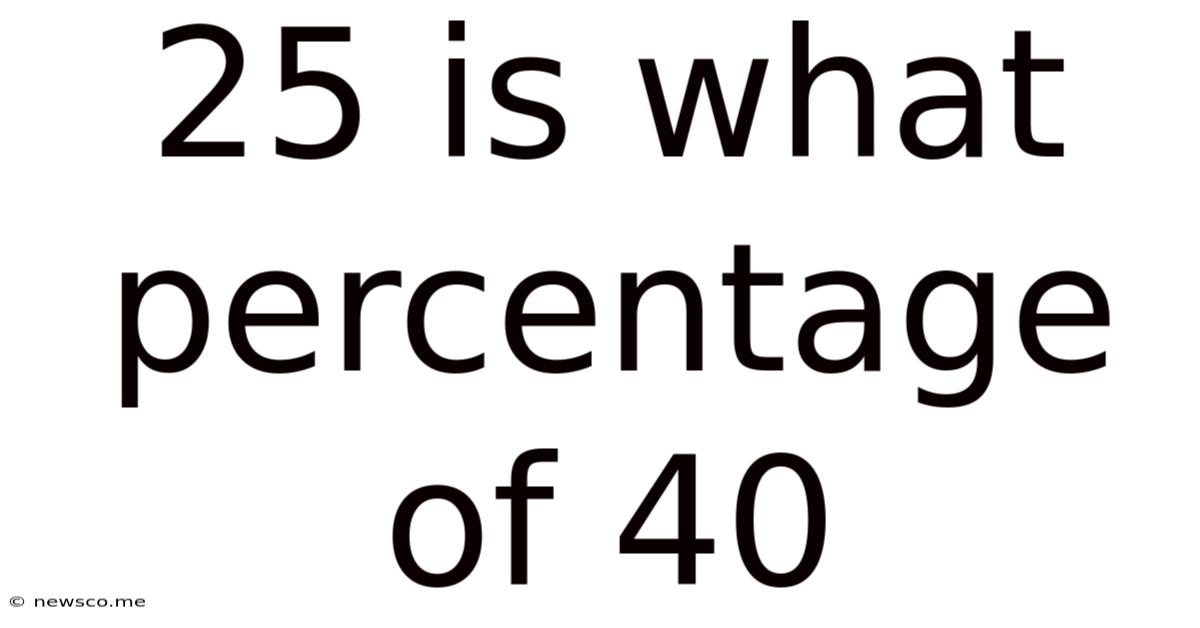
Table of Contents
25 is What Percentage of 40? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data accurately. This comprehensive guide will delve into the calculation of "25 is what percentage of 40?", exploring the underlying principles, offering multiple solution methods, and highlighting practical applications.
Understanding Percentages
Before jumping into the specific calculation, let's solidify our understanding of percentages. A percentage is simply a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% signifies 50 out of 100, which is equivalent to ½ or 0.5 in decimal form.
Method 1: The Proportion Method
This method uses the concept of proportions to solve percentage problems. We set up a proportion where one ratio represents the known values (25 and 40), and the other ratio represents the unknown percentage (x) and its base (100).
The setup:
25/40 = x/100
To solve for x (the percentage), we cross-multiply:
25 * 100 = 40 * x
2500 = 40x
Now, divide both sides by 40 to isolate x:
x = 2500 / 40
x = 62.5
Therefore, 25 is 62.5% of 40.
Method 2: The Decimal Method
This approach converts the fraction into a decimal and then multiplies by 100 to express it as a percentage.
The steps:
-
Form a fraction: Represent the problem as a fraction: 25/40
-
Convert to decimal: Divide 25 by 40: 25 ÷ 40 = 0.625
-
Multiply by 100: Multiply the decimal by 100 to convert it into a percentage: 0.625 * 100 = 62.5
Therefore, 25 is 62.5% of 40.
Method 3: Using a Calculator
Most calculators have a percentage function. The exact steps might vary depending on the calculator model, but the general process is:
-
Divide: Divide 25 by 40 (25 ÷ 40).
-
Multiply by 100: Multiply the result by 100.
The calculator will directly display the answer: 62.5%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios:
1. Finance and Budgeting:
- Calculating discounts: If a $40 item is discounted by 25%, you can quickly determine the discount amount ($10) and the final price ($30).
- Understanding interest rates: Calculating interest earned on savings accounts or interest accrued on loans involves percentage calculations.
- Analyzing financial statements: Percentage changes in revenue, expenses, and profits are vital for evaluating a business's financial health.
2. Retail and Sales:
- Determining markups and margins: Retailers use percentages to calculate the markup on products to achieve a desired profit margin.
- Calculating sales tax: Sales tax is a percentage added to the price of goods and services.
- Analyzing sales data: Businesses use percentages to track sales performance, compare sales figures across different periods, and identify trends.
3. Education and Statistics:
- Calculating grades: Many grading systems are based on percentages, converting raw scores into letter grades.
- Interpreting statistical data: Percentages are essential for representing and interpreting data in various statistical analyses. For example, expressing survey results as percentages makes them easier to understand and compare.
- Understanding test scores: Scores on standardized tests and academic assessments are often expressed as percentages.
4. Science and Engineering:
- Calculating efficiency: The efficiency of machines and processes is frequently expressed as a percentage.
- Analyzing experimental data: Percentage changes in measurements are often used to analyze the results of scientific experiments.
- Expressing concentrations: In chemistry, concentrations of solutions are often expressed as percentages (e.g., weight percent, volume percent).
5. Everyday Life:
- Calculating tips: Determining a tip amount in a restaurant often involves calculating a percentage of the bill.
- Understanding sales and discounts: Percentages are used extensively in advertisements and promotions to showcase deals and discounts.
- Managing personal finances: Budgeting and tracking spending often involve using percentages to allocate funds for different categories.
Beyond the Basics: Advanced Percentage Calculations
While this guide focuses on the fundamental calculation of "25 is what percentage of 40?", understanding percentages extends to more complex scenarios:
- Calculating percentage increase or decrease: This involves determining the percentage change between two values.
- Finding the original value after a percentage change: This often involves working backward from a final value to find the initial value.
- Solving for an unknown value within a complex percentage problem: This might involve multiple steps and the application of algebraic principles.
Conclusion
Mastering percentage calculations is an invaluable skill that empowers you to navigate numerous situations in your personal and professional life. The simple yet powerful techniques outlined in this guide – the proportion method, the decimal method, and using a calculator – provide versatile approaches to tackling various percentage problems. Remember that the ability to understand and apply percentages extends far beyond simple calculations; it unlocks a deeper understanding of data, financial matters, and numerous other areas. By mastering these fundamental concepts, you'll enhance your analytical skills and confidently approach numerical challenges in diverse contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about 25 Is What Percentage Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.