25 Of What Number Is 20
News Co
Apr 26, 2025 · 4 min read
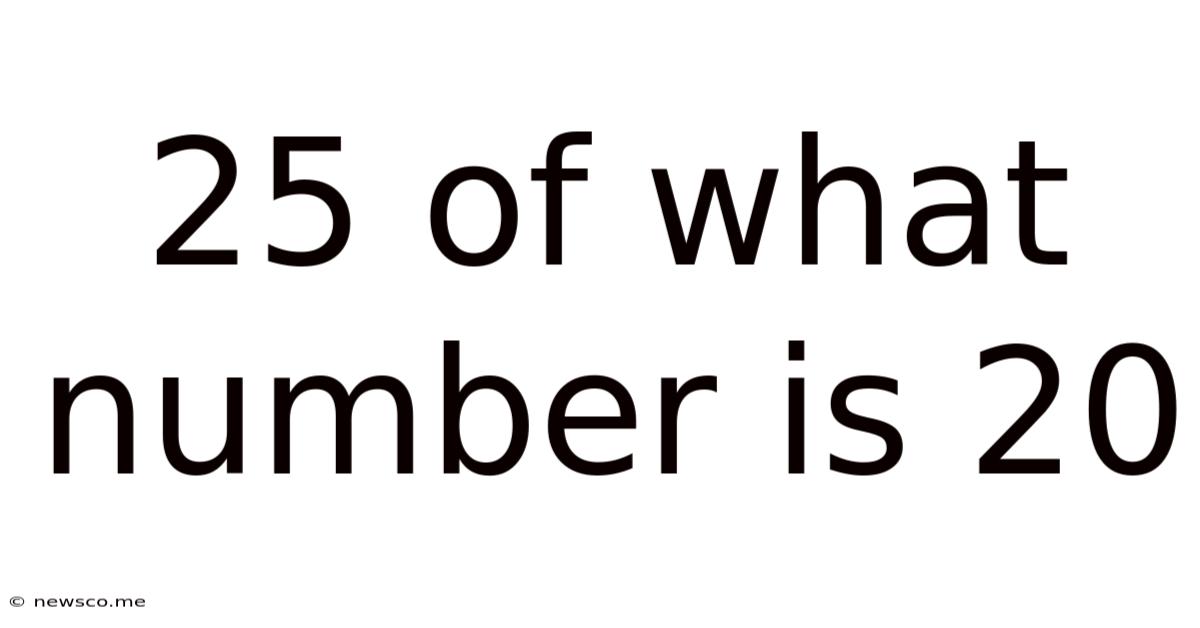
Table of Contents
25% of What Number is 20? Solving Percentage Problems
Finding out "25% of what number is 20" involves understanding and applying the principles of percentages. This seemingly simple question opens the door to a broader understanding of percentage calculations, crucial in various fields from everyday budgeting to advanced financial modeling. Let's explore several methods to solve this problem and delve into the underlying mathematical concepts.
Understanding Percentages
A percentage is a fraction or ratio expressed as a part of 100. The symbol "%" represents "percent," meaning "per hundred." For example, 25% can be written as a fraction (25/100) or a decimal (0.25). Understanding this fundamental concept is key to solving percentage problems.
Key Terms and Concepts:
- Percentage: A portion of a whole, represented as a number out of 100.
- Base (or Whole): The total amount or the number from which the percentage is calculated. This is what we're trying to find in our problem.
- Part (or Portion): The specific amount that represents the percentage of the whole. In our problem, the part is 20.
- Rate: The percentage itself (in our case, 25%).
Method 1: Using the Formula
The most common way to solve percentage problems is to use the basic percentage formula:
Part = (Rate/100) x Base
In our case:
- Part = 20
- Rate = 25
- Base = ? (This is what we need to find)
Let's substitute the known values into the formula:
20 = (25/100) x Base
Now, we solve for the Base:
- Simplify the fraction: 25/100 simplifies to 1/4.
- Rewrite the equation: 20 = (1/4) x Base
- Multiply both sides by 4: 20 x 4 = Base
- Solve for Base: Base = 80
Therefore, 25% of 80 is 20.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. A proportion sets up an equivalence between two ratios. We can set up a proportion using the given information:
25/100 = 20/x (where x represents the unknown base)
This proportion reads: "25 is to 100 as 20 is to x."
To solve this proportion:
- Cross-multiply: 25 * x = 100 * 20
- Simplify: 25x = 2000
- Solve for x: x = 2000 / 25
- Calculate: x = 80
Again, we find that the base is 80.
Method 3: Using Decimal Equivalents
As mentioned earlier, percentages can be expressed as decimals. 25% is equivalent to 0.25. We can rewrite the problem as:
0.25 x Base = 20
To solve for the base:
- Divide both sides by 0.25: Base = 20 / 0.25
- Calculate: Base = 80
Practical Applications of Percentage Calculations
Understanding percentage calculations extends far beyond simple math problems. Here are some real-world applications:
1. Finance and Budgeting:
- Calculating interest: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding how to calculate interest is essential for financial planning.
- Analyzing financial statements: Businesses use percentages to analyze financial data, such as profit margins, expense ratios, and return on investment (ROI).
- Calculating discounts and sales tax: Discounts and sales taxes are often expressed as percentages, making percentage calculations crucial for shopping and budgeting.
2. Science and Statistics:
- Analyzing data: Scientists and statisticians use percentages to represent data and draw conclusions from experiments and surveys.
- Calculating probabilities: Probability is often expressed as a percentage, allowing for easier understanding and comparison of likelihoods.
3. Everyday Life:
- Calculating tips: Waitstaff tips are often calculated as a percentage of the bill.
- Determining nutritional information: Nutritional labels show percentages of daily recommended values for various nutrients.
- Understanding sales and discounts: Sales and discounts are commonly advertised as percentages.
Beyond the Basics: More Complex Percentage Problems
While "25% of what number is 20?" is a straightforward problem, the principles involved can be applied to more complex scenarios. Consider these examples:
- Finding the percentage increase or decrease: Calculating the percentage change between two values requires understanding percentage calculations.
- Calculating compound interest: Compound interest involves repeated percentage calculations over time.
- Solving problems involving multiple percentages: Problems involving consecutive percentages or combined percentages require a deeper understanding of percentage operations.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill applicable in numerous contexts. By understanding the underlying concepts and utilizing the various methods outlined—the formula, proportions, and decimal equivalents—you can confidently tackle a wide range of percentage problems. The ability to solve percentage problems efficiently is not just beneficial for academic pursuits but also essential for making informed decisions in personal finance, professional settings, and everyday life. Remember that consistent practice is key to solidifying your understanding and building your problem-solving skills. From simple questions like "25% of what number is 20?" to more complex financial analyses, a strong grasp of percentages will serve you well.
Latest Posts
Related Post
Thank you for visiting our website which covers about 25 Of What Number Is 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.