25 Of What Number Is 60
News Co
May 07, 2025 · 4 min read
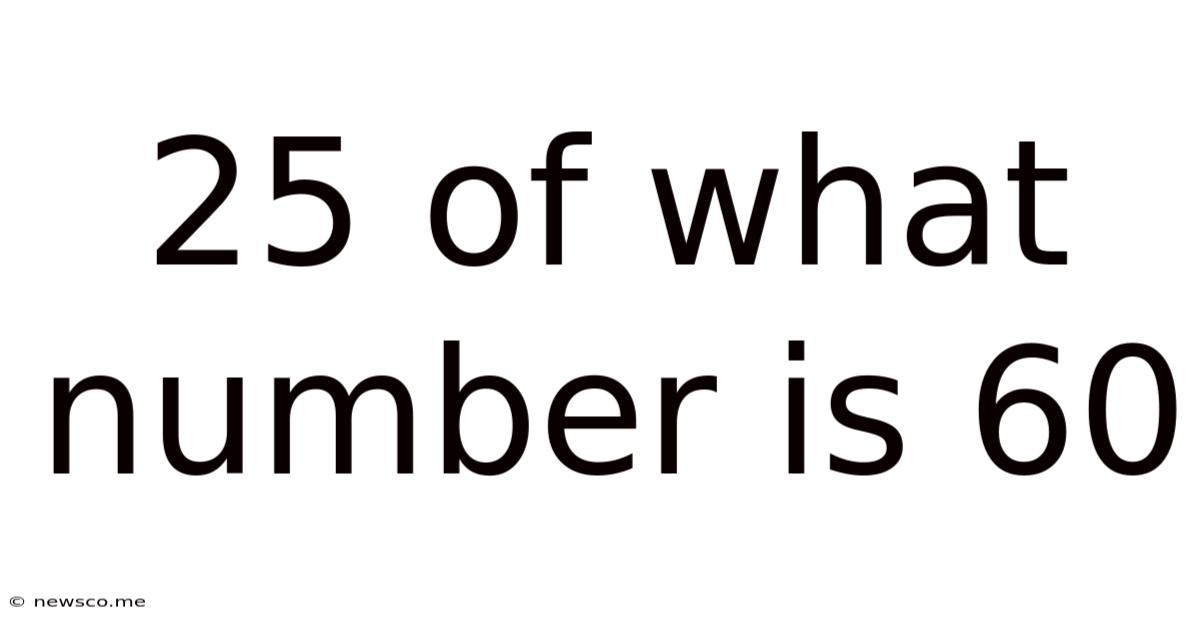
Table of Contents
25% of What Number is 60? A Deep Dive into Percentage Calculations
Finding the answer to "25% of what number is 60?" might seem straightforward, but understanding the underlying concepts opens the door to solving a wide variety of percentage problems. This article will not only provide the solution but also explore the various methods to solve this type of problem, explaining the reasoning behind each approach and offering practical applications for real-world scenarios.
Understanding Percentages
Before diving into the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. For example, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. This representation is crucial for understanding how percentages relate to whole numbers.
Key Concepts:
- Part: The portion of the whole that we're dealing with (in this case, 60).
- Percentage: The rate or proportion expressed as a fraction of 100 (25%).
- Whole: The total amount we're trying to find (our unknown value).
Method 1: Using Algebraic Equations
This method offers a structured approach, particularly useful for more complex percentage problems. We can translate the problem into an algebraic equation:
- Let 'x' represent the unknown whole number.
- 25% of x is 60 can be written as: 0.25x = 60
To solve for x, we isolate the variable by dividing both sides of the equation by 0.25:
- x = 60 / 0.25
- x = 240
Therefore, 25% of 240 is 60.
Method 2: Using Fractions
Since 25% is equivalent to 1/4, we can rewrite the problem as:
- (1/4) * x = 60
To solve for x, we multiply both sides by 4:
- x = 60 * 4
- x = 240
Again, we arrive at the same solution: 240
Method 3: Using Proportions
Proportions offer a visual and intuitive method for solving percentage problems. We can set up a proportion using the relationship between the part, the percentage, and the whole:
- Part / Whole = Percentage / 100
Substituting the known values:
- 60 / x = 25 / 100
To solve for x, we can cross-multiply:
- 60 * 100 = 25 * x
- 6000 = 25x
- x = 6000 / 25
- x = 240
This method reinforces the relationship between the parts and the whole, offering another clear path to the solution: 240
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in various aspects of daily life and professional settings. Here are some examples:
1. Sales and Discounts:
Imagine a store offering a 25% discount on an item. If the discounted price is $60, the original price can be calculated using the same methods described above. The original price was $80.
2. Financial Calculations:
Percentage calculations are fundamental in finance. Calculating interest rates, returns on investments, and tax percentages all rely on this skill. For instance, figuring out the principal amount based on the interest earned or the total amount after taxes.
3. Statistical Analysis:
Percentages are commonly used to represent data in statistical analysis. For example, expressing survey results or the proportion of a particular group within a larger population.
4. Scientific Calculations:
Many scientific calculations rely on expressing data as percentages. For example, in chemistry calculating the percentage composition of a compound or in biology describing the percentage growth of a population.
5. Everyday Budgeting:
Percentage calculations are essential when creating and managing a household budget. Determining what percentage of income is allocated to different expenses, tracking savings progress, and calculating expenses against income.
Beyond the Basics: Solving More Complex Percentage Problems
The fundamental principles applied to solve "25% of what number is 60?" can be extended to more complex problems. These might involve:
- Multiple percentages: Calculating the effect of successive percentage increases or decreases.
- Unknown percentages: Determining the percentage when the part and the whole are known.
- Compound interest: Calculating the final amount after applying interest over multiple periods.
Tips for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more comfortable you'll become with different problem types.
- Use different methods: Try each method (algebraic equations, fractions, proportions) to find the approach you find most intuitive.
- Check your work: Always verify your answers using a different method to ensure accuracy.
- Understand the concepts: Focus on understanding the underlying principles rather than memorizing formulas.
Conclusion
Solving "25% of what number is 60?" is a stepping stone to mastering percentage calculations. By understanding the various approaches – algebraic equations, fractions, and proportions – and applying them to real-world scenarios, you'll build a solid foundation for tackling more complex percentage problems. Remember, consistent practice and a clear understanding of the underlying principles are key to mastering this essential skill. The answer, as we've demonstrated through multiple methods, remains consistently 240.
Latest Posts
Latest Posts
-
Solving An Equation Written In Factored Form
May 08, 2025
-
Write The Number 0 0005 In Scientific Notation
May 08, 2025
-
Addition Property Of Equality In Geometry
May 08, 2025
-
Write 6 As A Fraction In Simplest Form
May 08, 2025
-
How Many Ml Is One Gallon
May 08, 2025
Related Post
Thank you for visiting our website which covers about 25 Of What Number Is 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.