2x 3 X 2 X 3
News Co
May 08, 2025 · 5 min read
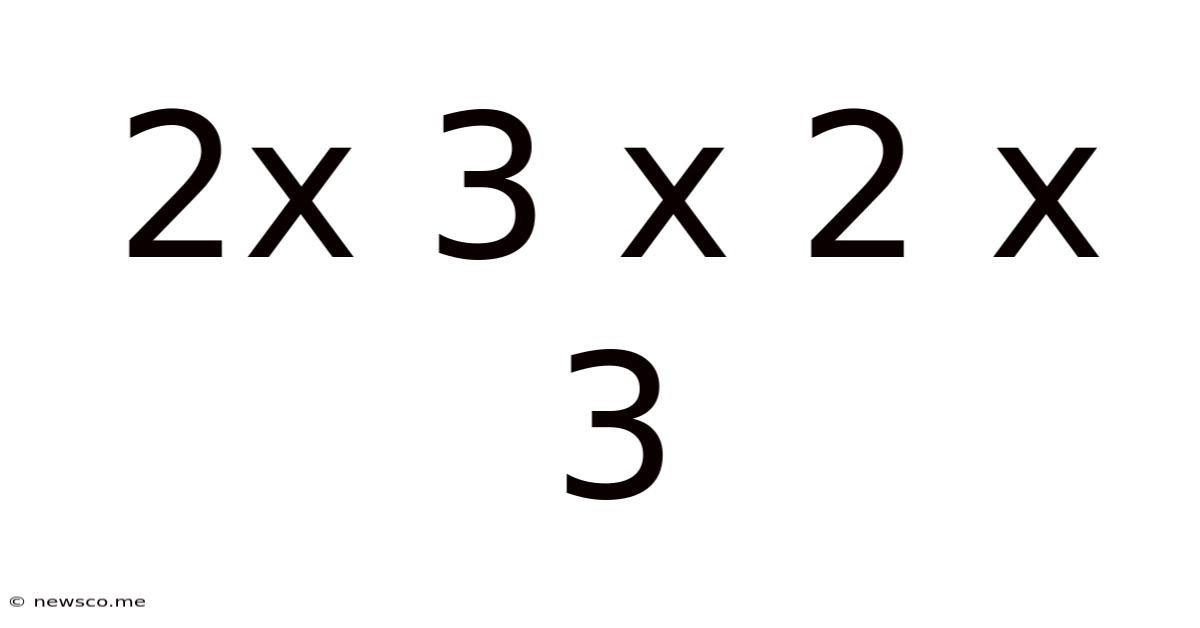
Table of Contents
Decomposing 2 x 3 x 2 x 3: A Deep Dive into Factorization, Prime Numbers, and Mathematical Applications
The seemingly simple expression "2 x 3 x 2 x 3" opens a door to a fascinating world of mathematical concepts. While the immediate answer – 36 – is straightforward, exploring the underlying structure reveals deeper insights into prime factorization, commutative and associative properties, and the broader applications of these principles in various fields. This article delves into these aspects, showcasing how a seemingly simple calculation can illuminate complex mathematical ideas.
Understanding Prime Factorization
At the heart of this expression lies the concept of prime factorization. Prime numbers, the building blocks of all other whole numbers, are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...). The prime factorization of a number is the unique representation of that number as a product of its prime factors.
In our case, 2 x 3 x 2 x 3 is already presented as a factorization. However, we can refine this by grouping like terms:
2 x 2 x 3 x 3 = 2² x 3²
This representation, 2² x 3², is the prime factorization of 36. It tells us that 36 is composed of two factors of 2 and two factors of 3. This unique factorization is crucial in various mathematical operations and applications.
Commutative and Associative Properties
The expression 2 x 3 x 2 x 3 highlights the commutative property of multiplication. The commutative property states that the order of factors doesn't affect the product. We can rearrange the factors in any order, and the result will always be 36:
- 2 x 2 x 3 x 3 = 36
- 3 x 2 x 3 x 2 = 36
- 3 x 3 x 2 x 2 = 36
- and so on...
Similarly, the associative property of multiplication demonstrates that the grouping of factors doesn't change the product. We can group the factors differently using parentheses without altering the outcome:
- (2 x 3) x (2 x 3) = 36
- (2 x 2) x (3 x 3) = 36
- 2 x (3 x 2 x 3) = 36
These properties are fundamental to simplifying complex expressions and performing calculations efficiently. They underpin many advanced mathematical concepts and algorithms.
Applications of Prime Factorization and Related Concepts
The seemingly simple act of decomposing 2 x 3 x 2 x 3 into its prime factors has far-reaching implications in diverse fields:
1. Cryptography
Prime factorization plays a crucial role in modern cryptography, especially in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring large numbers into their prime components. The larger the numbers, the more computationally intensive the factorization becomes, making it practically impossible to crack the encryption within a reasonable timeframe.
2. Number Theory
Prime factorization forms the bedrock of number theory, a branch of mathematics that deals with the properties of integers. Concepts like the greatest common divisor (GCD) and the least common multiple (LCM) are directly related to prime factorization. Understanding these concepts is crucial for solving various number-theoretic problems.
3. Algebra
In algebra, factorization is a critical tool for simplifying and solving equations. Expressing polynomials as products of their factors often makes it easier to find solutions or understand the behavior of the polynomial. Prime factorization extends this principle to the realm of integers.
4. Computer Science
Prime factorization and related algorithms are used in various computer science applications, including:
- Hashing: Prime numbers are often used in hash functions to minimize collisions and distribute data more evenly.
- Data Structures: Prime numbers are sometimes employed in the design of certain data structures to improve efficiency.
- Algorithm Analysis: Understanding the complexity of prime factorization algorithms is essential for assessing the performance of cryptographic systems and other computational processes.
5. Combinatorics and Probability
Prime factorization can indirectly influence calculations in combinatorics and probability. When dealing with factorial calculations (n!), prime factorization can simplify certain computations and provide insights into the structure of the problem.
Beyond 36: Exploring Variations and Extensions
While we've focused on 2 x 3 x 2 x 3, we can extend these concepts to explore variations and broader implications. Consider these related questions:
-
What if we add another factor? Let's add a 5: 2 x 3 x 2 x 3 x 5 = 180. How does the introduction of a new prime factor affect the prime factorization and overall value? This showcases the building-block nature of primes in constructing larger numbers.
-
What if we change the factors? Consider 2 x 5 x 7 x 11. What are the prime factors? What is the resulting product? This emphasizes the unique composition of each number based on its prime factors.
-
Finding the LCM and GCD: Let's compare 2 x 3 x 2 x 3 (36) with another number, say 2 x 2 x 5 (20). Finding the least common multiple (LCM) and greatest common divisor (GCD) of 36 and 20 using their prime factorizations will illustrate the practical applications of this method in number theory. The LCM would be 2² x 3² x 5 = 180, and the GCD would be 2².
-
Exploring larger numbers: Prime factorization of larger numbers becomes computationally challenging. This is a key factor in the security of cryptographic systems, highlighting the practical implications of this mathematical concept in real-world applications.
Conclusion: The Power of Simplicity
The expression 2 x 3 x 2 x 3, seemingly simple at first glance, unveils a rich tapestry of mathematical concepts. Through prime factorization, we uncover the building blocks of numbers, explore fundamental properties like commutativity and associativity, and glimpse the profound implications of these concepts in cryptography, number theory, algebra, computer science, and beyond. This exploration emphasizes the power of delving into seemingly simple mathematical expressions to unearth a wealth of knowledge and understanding, ultimately highlighting the interconnectedness and beauty of mathematics. The ability to decompose and analyze numbers in this way is a fundamental skill, useful in numerous fields and furthering our understanding of the world around us.
Latest Posts
Latest Posts
-
Is The Square Root Of 81 Rational
May 08, 2025
-
A Polygon With 5 Sides Is Called A
May 08, 2025
-
120 Do F Bang Bao Nhieu Do C
May 08, 2025
-
Cuanto Son 40 Grados Celsius En Fahrenheit
May 08, 2025
-
Multiplication Chart All The Way To 20
May 08, 2025
Related Post
Thank you for visiting our website which covers about 2x 3 X 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.