2x 3y 9 In Slope Intercept Form
News Co
Apr 17, 2025 · 5 min read
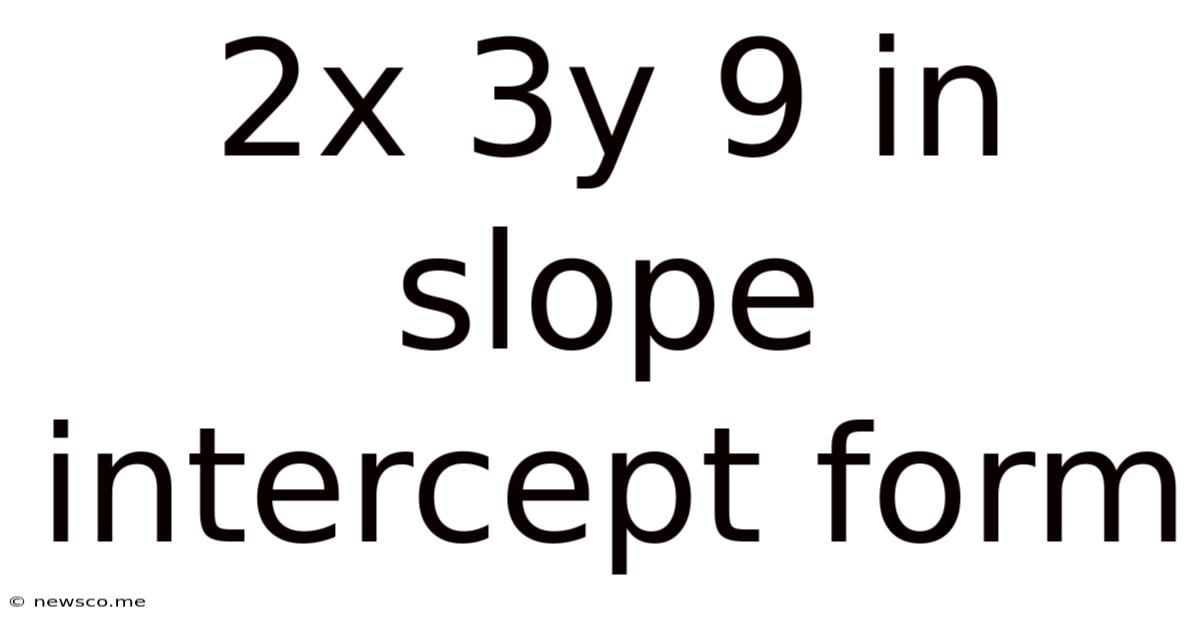
Table of Contents
Transforming 2x + 3y = 9 into Slope-Intercept Form: A Comprehensive Guide
The equation 2x + 3y = 9 represents a linear relationship between two variables, x and y. While useful in its current form, converting it to slope-intercept form (y = mx + b) offers significant advantages in understanding and visualizing the line it represents. This form explicitly reveals the slope (m) and the y-intercept (b) of the line, providing valuable insights into its characteristics. This comprehensive guide will delve into the process of this transformation, exploring the underlying concepts and offering practical examples.
Understanding Slope-Intercept Form (y = mx + b)
Before we embark on the conversion, let's solidify our understanding of the slope-intercept form, y = mx + b.
- y: Represents the dependent variable, typically plotted on the vertical axis of a graph.
- x: Represents the independent variable, typically plotted on the horizontal axis.
- m: Represents the slope of the line. The slope describes the steepness and direction of the line. A positive slope indicates an upward trend from left to right, while a negative slope indicates a downward trend. The slope is calculated as the change in y divided by the change in x (rise over run).
- b: Represents the y-intercept, which is the point where the line intersects the y-axis (where x = 0).
Steps to Convert 2x + 3y = 9 to Slope-Intercept Form
The conversion process involves isolating 'y' on one side of the equation. Here's a step-by-step breakdown:
-
Start with the original equation: 2x + 3y = 9
-
Subtract 2x from both sides: This isolates the term containing 'y'. 3y = -2x + 9
-
Divide both sides by 3: This isolates 'y', giving us the slope-intercept form. y = (-2/3)x + 3
Therefore, the slope-intercept form of the equation 2x + 3y = 9 is y = (-2/3)x + 3.
Interpreting the Slope and Y-Intercept
Now that we have the equation in slope-intercept form, we can easily extract valuable information:
-
Slope (m = -2/3): This indicates a negative slope. The line will slant downwards from left to right. The slope of -2/3 means that for every 3 units increase in x, y decreases by 2 units.
-
Y-intercept (b = 3): This tells us that the line intersects the y-axis at the point (0, 3). This is a crucial point for graphing the line.
Graphing the Line
With the slope and y-intercept in hand, graphing the line becomes straightforward:
-
Plot the y-intercept: Place a point at (0, 3) on the y-axis.
-
Use the slope to find another point: The slope is -2/3. From the y-intercept (0, 3), move 3 units to the right (positive x-direction) and 2 units down (negative y-direction). This gives you a second point at (3, 1).
-
Draw the line: Draw a straight line through the two points you've plotted. This line represents the equation 2x + 3y = 9.
Practical Applications and Real-World Examples
The ability to transform equations into slope-intercept form has numerous applications across various fields:
-
Economics: Linear equations are frequently used to model supply and demand relationships. The slope-intercept form helps analyze the price elasticity of demand and the responsiveness of supply to changes in price.
-
Physics: In kinematics, the equation of motion for constant velocity can be represented in slope-intercept form, where the slope represents the velocity and the y-intercept represents the initial position.
-
Engineering: Linear equations are used to model relationships between variables in various engineering disciplines. The slope-intercept form helps in analyzing system behavior and predicting outcomes.
-
Computer Science: Linear equations are fundamental in computer graphics and image processing, where they are used to represent lines and transformations.
-
Finance: Linear equations can be used to model financial growth, depreciation, and investment returns. The slope-intercept form helps in analyzing trends and making predictions.
Advanced Concepts and Extensions
While we've focused on the basic conversion, it's important to understand some advanced concepts:
-
Parallel and Perpendicular Lines: Lines with the same slope are parallel. Lines with slopes that are negative reciprocals of each other are perpendicular. Knowing the slope from the slope-intercept form allows you to quickly determine the relationship between different lines.
-
Finding the x-intercept: While the y-intercept is readily available, the x-intercept (where the line crosses the x-axis) can be found by setting y = 0 in the original equation or the slope-intercept form and solving for x. In this case, setting y = 0 in y = (-2/3)x + 3 gives x = 4.5, meaning the x-intercept is (4.5, 0).
-
Equations with No Slope (Vertical Lines): Equations of the form x = c (where c is a constant) represent vertical lines. These lines have undefined slopes because the change in x is zero, resulting in division by zero. They cannot be expressed in slope-intercept form.
-
Equations with Zero Slope (Horizontal Lines): Equations of the form y = c (where c is a constant) represent horizontal lines. These lines have a slope of zero, indicating no change in y as x changes.
Troubleshooting Common Mistakes
Here are some common mistakes to avoid when converting equations:
-
Incorrectly applying the order of operations: Always follow the order of operations (PEMDAS/BODMAS) when simplifying equations.
-
Making errors in algebraic manipulation: Double-check each step to ensure accuracy. A single mistake can lead to an incorrect slope-intercept form.
-
Forgetting to divide by the coefficient of y: A crucial step in isolating 'y' is dividing both sides of the equation by its coefficient. Failing to do this will lead to an incorrect result.
-
Misinterpreting the slope and y-intercept: Pay close attention to the signs and values of the slope and y-intercept to accurately graph and analyze the line.
Conclusion: Mastering Slope-Intercept Form
Converting equations from standard form to slope-intercept form is a fundamental skill in algebra and has wide-ranging applications in various fields. By understanding the process, interpreting the slope and y-intercept, and avoiding common errors, you'll gain a powerful tool for analyzing linear relationships and visualizing data. The ability to easily manipulate and interpret these equations is essential for anyone working with data or modeling linear relationships. This thorough guide equips you with the knowledge and understanding necessary to confidently tackle these conversions and apply them to real-world problems. Remember to practice regularly to solidify your understanding and enhance your problem-solving skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2x 3y 9 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.