3 4 Divided By 2 3 In Fraction Form
News Co
May 04, 2025 · 5 min read
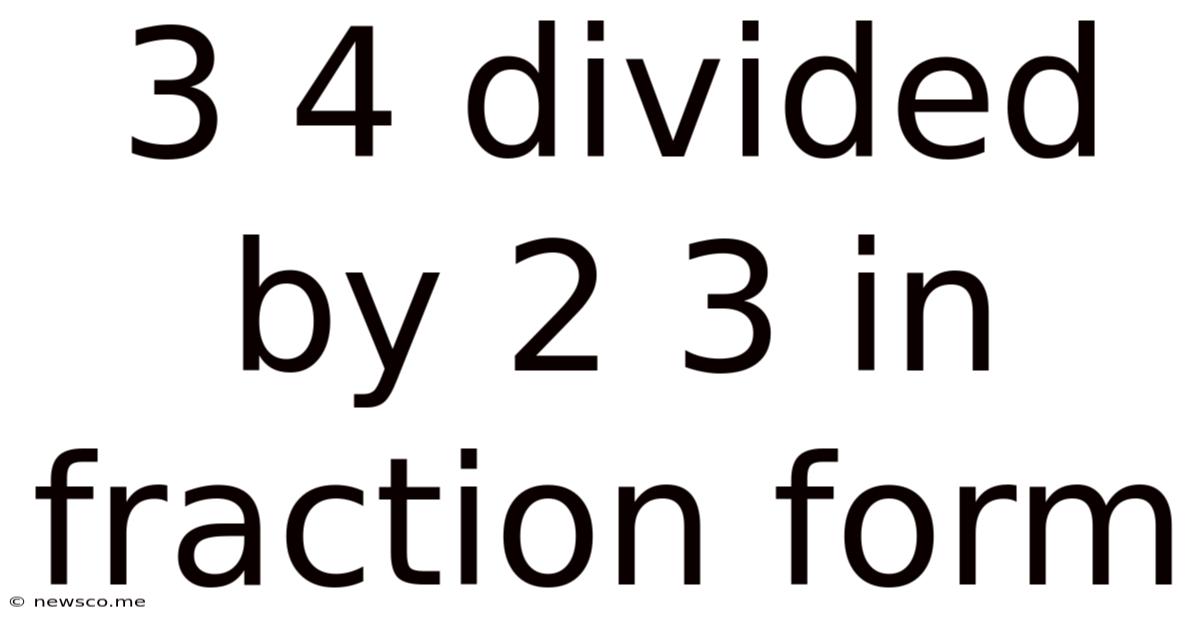
Table of Contents
3/4 Divided by 2/3 in Fraction Form: A Comprehensive Guide
Understanding fraction division can be tricky, but mastering it unlocks a world of mathematical possibilities. This comprehensive guide will walk you through the process of dividing 3/4 by 2/3, explaining the steps, the underlying principles, and offering various approaches to help you confidently tackle similar problems. We'll delve into the "why" behind the method, not just the "how," solidifying your understanding of fraction manipulation.
Understanding Fraction Division: The "Invert and Multiply" Rule
The most common method for dividing fractions involves a crucial step: inverting the second fraction (the divisor) and then multiplying. This seemingly simple trick is rooted in the fundamental concept of reciprocal numbers. Two numbers are reciprocals if their product equals 1. For example, the reciprocal of 2/3 is 3/2, because (2/3) * (3/2) = 1.
This "invert and multiply" rule is not arbitrary; it's derived from the definition of division itself. Dividing by a number is the same as multiplying by its reciprocal. Let's illustrate this:
- a ÷ b = a * (1/b)
This equation shows that dividing 'a' by 'b' is equivalent to multiplying 'a' by the reciprocal of 'b'. This is the core principle behind the "invert and multiply" method.
Step-by-Step Solution: 3/4 ÷ 2/3
Now, let's apply this knowledge to our problem: 3/4 ÷ 2/3.
Step 1: Invert the second fraction (the divisor).
The divisor is 2/3. Its reciprocal is 3/2.
Step 2: Change the division sign to a multiplication sign.
Our problem now becomes: 3/4 * 3/2
Step 3: Multiply the numerators (top numbers) together.
3 * 3 = 9
Step 4: Multiply the denominators (bottom numbers) together.
4 * 2 = 8
Step 5: Simplify the resulting fraction, if possible.
Our result is 9/8. This fraction is already in its simplest form because the greatest common divisor of 9 and 8 is 1. We can, however, express it as a mixed number:
9/8 = 1 1/8
Therefore, 3/4 divided by 2/3 equals 9/8 or 1 1/8.
Visualizing Fraction Division with Models
Understanding fractions can be significantly easier when we visualize them. Let's use a visual model to understand 3/4 ÷ 2/3. Imagine a rectangle representing one whole unit.
-
Represent 3/4: Divide the rectangle into four equal parts and shade three of them. This represents 3/4.
-
Divide 3/4 into groups of 2/3: This is where it gets interesting. We want to find out how many groups of 2/3 fit into 3/4. This requires some creative visualization. You might find it helpful to further subdivide your rectangle to create smaller, equal units that can be used to represent both 3/4 and 2/3.
-
Counting the Groups: After carefully subdividing and counting, you'll find that approximately 1 and 1/8 groups of 2/3 fit into 3/4. This aligns perfectly with our calculated answer of 1 1/8.
This visual approach helps solidify the abstract concept of fraction division, making it more intuitive and memorable.
Alternative Methods for Dividing Fractions
While the "invert and multiply" method is the most common and efficient, other approaches can reinforce understanding:
Method 2: Using Common Denominators
This method involves finding a common denominator for both fractions and then dividing the numerators.
-
Find a common denominator: The least common multiple of 4 and 3 is 12.
-
Convert fractions to equivalent fractions with the common denominator:
- 3/4 = 9/12
- 2/3 = 8/12
-
Divide the numerators: 9 ÷ 8 = 9/8
This method yields the same result: 9/8 or 1 1/8. However, it can be more computationally intensive for larger numbers.
Method 3: Converting to Decimals (Approximation)
Converting fractions to decimals provides an approximate solution. This approach is useful for quick estimations but lacks the precision of the fraction methods.
-
Convert fractions to decimals:
- 3/4 = 0.75
- 2/3 ≈ 0.6667
-
Divide the decimals: 0.75 ÷ 0.6667 ≈ 1.125
This decimal result is approximately equivalent to 1 1/8. Note the slight imprecision due to the rounding of the decimal representation of 2/3.
Practical Applications of Fraction Division
Fraction division is far from a purely theoretical exercise; it has many practical applications in everyday life and various fields:
-
Cooking and Baking: Scaling recipes up or down requires dividing fractions. For example, if a recipe calls for 1/2 cup of flour and you want to make half the recipe, you need to calculate 1/2 ÷ 2.
-
Sewing and Crafting: Cutting fabric or other materials accurately involves working with fractional measurements and dividing them.
-
Construction and Engineering: Precision in construction requires accurate calculations involving fractions and their divisions, ensuring structural integrity and functionality.
-
Data Analysis and Statistics: Fraction division is crucial in interpreting data, calculating proportions, and understanding statistical distributions.
-
Financial Calculations: Dividing fractions is essential in various financial calculations, such as calculating proportions of investments or determining fractional shares.
Troubleshooting Common Mistakes in Fraction Division
Several common errors can occur when dividing fractions:
-
Forgetting to invert the divisor: This is the most frequent mistake. Remember to always invert the second fraction before multiplying.
-
Incorrect multiplication of numerators and denominators: Double-check your multiplication to avoid simple arithmetic errors.
-
Failing to simplify the final fraction: Always simplify your answer to its lowest terms to represent the most accurate and concise solution.
Expanding Your Understanding: More Complex Fraction Problems
Once you've mastered the basics of dividing simple fractions, you can tackle more complex problems. These might involve:
-
Dividing mixed numbers: Convert mixed numbers to improper fractions before applying the "invert and multiply" rule.
-
Dividing fractions with different signs: Remember the rules of signed numbers: a positive divided by a negative is negative, and a negative divided by a negative is positive.
-
Dividing fractions with variables: The same principles apply, but the final answer will contain variables.
By practicing regularly and applying the techniques outlined above, you can build a strong foundation in fraction division and confidently tackle a wide range of mathematical problems. Remember, consistent practice is key to mastering this essential skill. Don't hesitate to work through numerous examples, and soon, you'll find fraction division as intuitive as addition and subtraction.
Latest Posts
Latest Posts
-
2 Step Equations Calculator With Fractions
May 05, 2025
-
Power Of A Power Property Examples
May 05, 2025
-
Square Root Of 3 Times Square Root Of 5
May 05, 2025
-
3 And 3 4 As A Decimal
May 05, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 2 3 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.