3/4 Divided By 3 As A Fraction
News Co
Apr 26, 2025 · 4 min read
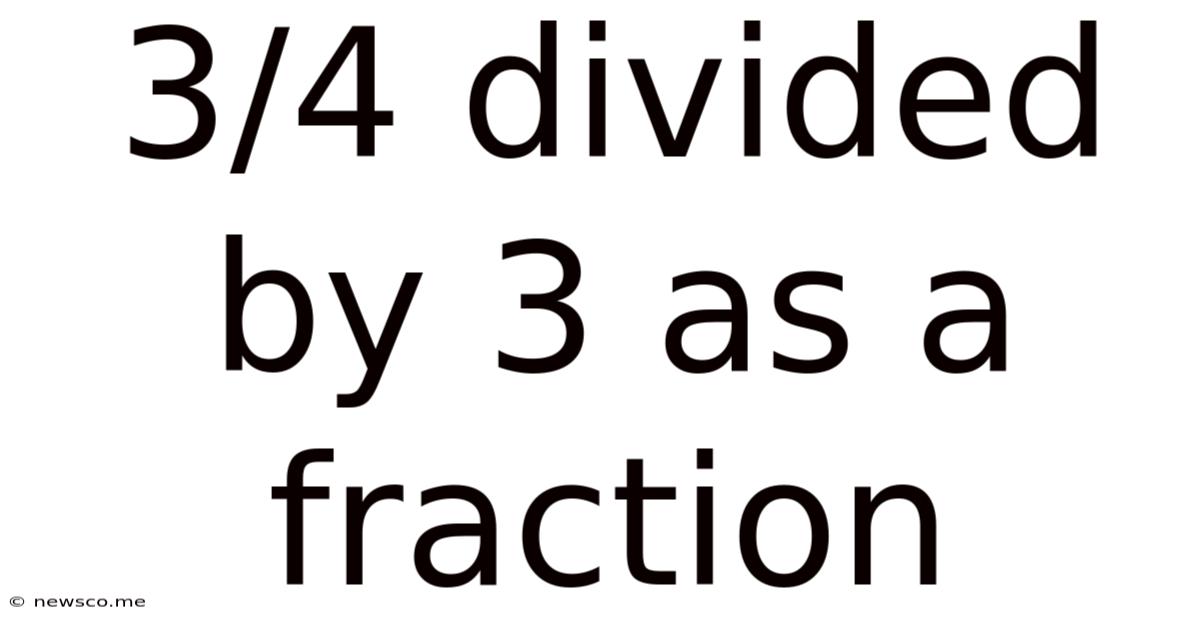
Table of Contents
3/4 Divided by 3: A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This article will delve into the intricacies of dividing 3/4 by 3, providing a comprehensive explanation, multiple approaches, and practical applications. We'll explore the underlying mathematical principles and offer tips for solving similar problems. By the end, you'll be confident in tackling fraction division with ease.
Understanding Fraction Division
Before tackling 3/4 divided by 3, let's establish the fundamental principles of fraction division. The core concept revolves around the idea of reciprocals (also known as multiplicative inverses). The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
Dividing by a fraction is equivalent to multiplying by its reciprocal. This crucial understanding forms the basis of our solution. This means that instead of dividing by a fraction, we can multiply by its reciprocal, simplifying the calculation considerably.
Method 1: The Reciprocal Method
This is the most common and efficient method for dividing fractions. To divide 3/4 by 3, we first express the whole number 3 as a fraction: 3/1. Then, we change the division operation to multiplication by taking the reciprocal of the divisor (3/1).
Steps:
- Rewrite the problem: 3/4 ÷ 3/1
- Take the reciprocal of the divisor: The reciprocal of 3/1 is 1/3.
- Change division to multiplication: 3/4 x 1/3
- Multiply the numerators and denominators: (3 x 1) / (4 x 3) = 3/12
- Simplify the fraction: 3/12 simplifies to 1/4 by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 3.
Therefore, 3/4 divided by 3 is 1/4.
Method 2: Visual Representation
Visualizing fraction division can enhance understanding, especially for beginners. Imagine you have a pizza cut into four equal slices, representing 3/4 of the pizza. Now, you want to divide this 3/4 into three equal parts. Each of these three parts would represent 1/4 of the whole pizza.
This visual approach demonstrates that dividing 3/4 by 3 results in 1/4.
Method 3: Using Decimal Equivalents
While not always recommended for maintaining accuracy, converting fractions to decimals can provide an alternative approach.
Steps:
- Convert the fraction to a decimal: 3/4 = 0.75
- Divide the decimal by the whole number: 0.75 ÷ 3 = 0.25
- Convert the decimal back to a fraction: 0.25 = 1/4
This method confirms that 3/4 divided by 3 is indeed 1/4. However, remember that rounding errors can occur when using decimal conversions, especially with more complex fractions.
Practical Applications
Understanding fraction division is crucial in various real-world scenarios. Here are some examples:
- Cooking and Baking: Scaling down recipes often involves dividing fractions. If a recipe calls for 3/4 cup of flour, and you want to make only 1/3 of the recipe, you'll need to calculate (3/4) ÷ 3 to determine the required amount of flour.
- Sewing and Crafting: Cutting fabric or other materials often necessitates dividing fractions to obtain precise measurements.
- Construction and Engineering: Precise calculations involving fractions are vital in construction and engineering projects, ensuring accuracy and structural integrity.
- Data Analysis: Working with datasets often involves manipulating fractions and proportions. Dividing fractions is a common operation when dealing with statistical data.
Common Mistakes to Avoid
Several common mistakes can hinder accurate fraction division:
- Forgetting to take the reciprocal: This is the most frequent error. Remember, you must multiply by the reciprocal of the divisor, not the dividend.
- Incorrect simplification: Always simplify the resulting fraction to its lowest terms by finding the greatest common divisor of the numerator and denominator.
- Improper conversion to decimals: While sometimes helpful, decimal conversions can introduce rounding errors. It's best to stick to the reciprocal method for maximum accuracy, especially when dealing with complex fractions.
Expanding Your Understanding: More Complex Fraction Division
The principles discussed here can be applied to more complex fraction division problems. For example, consider dividing a fraction by another fraction:
(a/b) ÷ (c/d) = (a/b) x (d/c) = (a x d) / (b x c)
Always remember to take the reciprocal of the divisor (the second fraction) and then multiply the numerators and denominators. Simplify the resulting fraction to its lowest terms.
Conclusion: Mastering Fraction Division
Dividing fractions might seem challenging at first, but by mastering the reciprocal method and understanding the underlying principles, you can confidently tackle any fraction division problem. Remember to practice regularly, and don't hesitate to use visual aids to reinforce your understanding. With consistent practice and a clear grasp of the concepts, fraction division will become a manageable and essential skill in various academic and real-world applications. The ability to accurately and efficiently divide fractions is an invaluable asset, opening doors to more advanced mathematical concepts and problem-solving. So, embrace the challenge, practice diligently, and watch your confidence grow as you master this fundamental mathematical operation. By focusing on the reciprocal method and avoiding common pitfalls, you'll be well-equipped to handle fraction division with ease and precision.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3/4 Divided By 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.