3/4 Divided By 4 In Fraction
News Co
May 03, 2025 · 5 min read
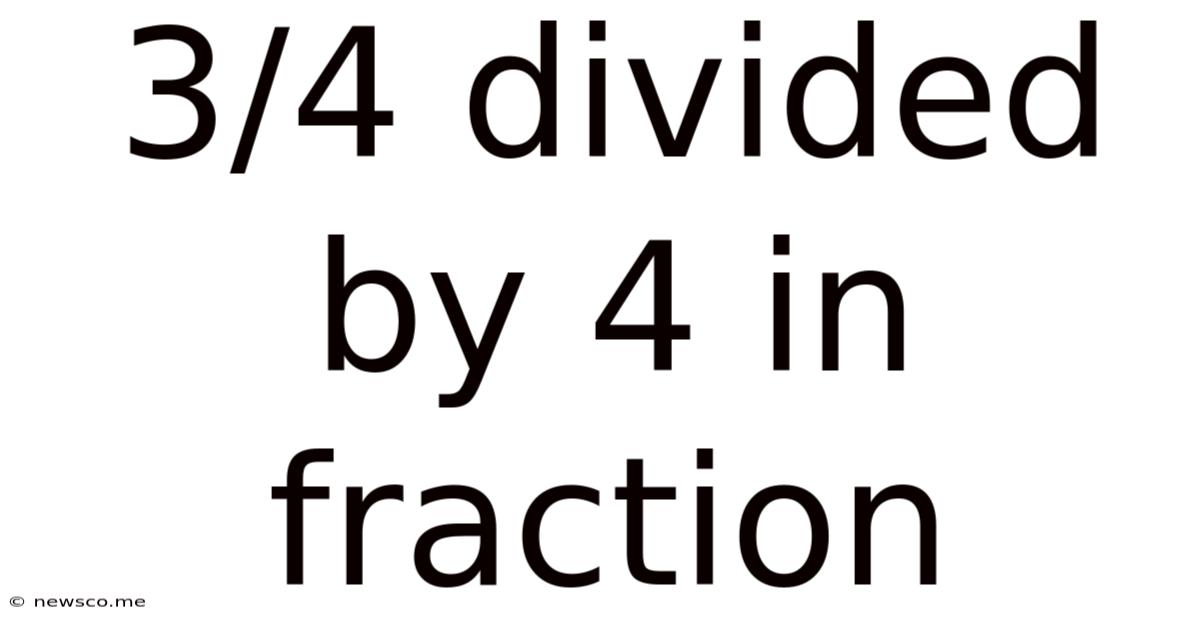
Table of Contents
3/4 Divided by 4: A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing the fraction 3/4 by 4, explaining the steps, the underlying principles, and offering practical examples to solidify your understanding. We'll explore various methods, ensuring you grasp the concept thoroughly.
Understanding Fraction Division
Before diving into the specific problem of 3/4 divided by 4, let's establish the fundamental principles of fraction division. The core concept revolves around the reciprocal. The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 4 is 1/4, the reciprocal of 2/3 is 3/2.
The golden rule of fraction division is: To divide a fraction by a whole number (or another fraction), we multiply the first fraction by the reciprocal of the second.
This seemingly simple rule underpins the entire process. Let's break it down further:
Reciprocals: The Key to Fraction Division
Understanding reciprocals is crucial. A reciprocal "flips" a fraction. The numerator becomes the denominator, and the denominator becomes the numerator. This "flipping" is the heart of the division process. It transforms a division problem into a multiplication problem, which is generally easier to manage.
- Example 1: The reciprocal of 5 (which can be written as 5/1) is 1/5.
- Example 2: The reciprocal of 2/7 is 7/2.
- Example 3: The reciprocal of 1/3 is 3/1, or simply 3.
From Division to Multiplication: The Transformation
The process of dividing fractions involves a two-step transformation:
- Find the reciprocal: Identify the divisor (the number you're dividing by) and find its reciprocal.
- Change to multiplication: Replace the division symbol (÷) with a multiplication symbol (×) and use the reciprocal you found in step 1.
Solving 3/4 Divided by 4
Now, let's apply these principles to solve the problem at hand: 3/4 divided by 4.
Step 1: Identify the reciprocal: The divisor is 4. The reciprocal of 4 (or 4/1) is 1/4.
Step 2: Change to multiplication: Rewrite the problem as a multiplication problem:
(3/4) × (1/4)
Step 3: Multiply the numerators and denominators:
Multiply the numerators (top numbers) together: 3 × 1 = 3 Multiply the denominators (bottom numbers) together: 4 × 4 = 16
This gives us the result: 3/16
Therefore, 3/4 divided by 4 equals 3/16.
Alternative Methods and Visual Representations
While the reciprocal method is the most efficient, other approaches can help solidify understanding.
Using Visual Representations
Imagine a pizza cut into four equal slices. You have three of those slices (3/4 of a pizza). Now, you want to divide those three slices equally among four people. Each person would get a much smaller portion. This visual representation intuitively demonstrates that the result will be a fraction smaller than 3/4.
The "Keep, Change, Flip" Method
This mnemonic device is helpful for remembering the steps:
- Keep: Keep the first fraction as it is (3/4).
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (4 becomes 1/4).
This leads to the same calculation: (3/4) × (1/4) = 3/16
Expanding on Fraction Division: More Complex Examples
Let's explore more complex scenarios to further reinforce the principles of fraction division.
Dividing a Fraction by Another Fraction
Consider dividing 2/5 by 3/7:
Step 1: Find the reciprocal of 3/7, which is 7/3.
Step 2: Change to multiplication: (2/5) × (7/3)
Step 3: Multiply numerators and denominators: (2 × 7) / (5 × 3) = 14/15
Therefore, 2/5 divided by 3/7 equals 14/15.
Dividing Mixed Numbers
Mixed numbers combine whole numbers and fractions (e.g., 1 1/2). To divide mixed numbers, first convert them into improper fractions.
Let's divide 2 1/3 by 1 1/2:
Step 1: Convert mixed numbers to improper fractions:
- 2 1/3 = (2 × 3 + 1) / 3 = 7/3
- 1 1/2 = (1 × 2 + 1) / 2 = 3/2
Step 2: Find the reciprocal of 3/2, which is 2/3.
Step 3: Change to multiplication: (7/3) × (2/3)
Step 4: Multiply numerators and denominators: (7 × 2) / (3 × 3) = 14/9
Therefore, 2 1/3 divided by 1 1/2 equals 14/9, which can be simplified to 1 5/9.
Simplifying Fractions: A Crucial Step
After performing the multiplication, always simplify your answer to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
For example, if you get 12/18, the GCD of 12 and 18 is 6. Dividing both by 6 gives you the simplified fraction 2/3.
Practical Applications of Fraction Division
Fraction division isn't just a theoretical exercise; it has numerous real-world applications:
- Cooking and Baking: Scaling recipes up or down requires dividing fractions.
- Sewing and Crafting: Cutting fabric or other materials accurately involves fraction calculations.
- Construction and Engineering: Precise measurements in construction rely heavily on fractions.
- Finance and Budgeting: Dividing resources and managing finances often involves fractional amounts.
Conclusion: Mastering Fraction Division
Understanding fraction division is a fundamental skill with wide-ranging applications. By mastering the concept of reciprocals and applying the "keep, change, flip" method, you can confidently tackle any fraction division problem. Remember to always simplify your answers to their lowest terms. Practice makes perfect – the more you work with fractions, the more comfortable and proficient you'll become. This comprehensive guide provides a solid foundation for tackling more complex fractional calculations and real-world problems involving fraction division. Through consistent practice and the application of the principles outlined here, you'll master this essential mathematical skill.
Latest Posts
Latest Posts
-
Do The Diagonals Of A Rhombus Bisect The Angles
May 07, 2025
-
How Long Is 84 Weeks In Months
May 07, 2025
-
3 Liters To Glasses Of Water
May 07, 2025
-
Write The Value Of The Underlined Digit Decimal
May 07, 2025
-
What Are The Multiples Of 23
May 07, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Divided By 4 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.