3 4 Divided By 6 In Fraction
News Co
May 08, 2025 · 4 min read
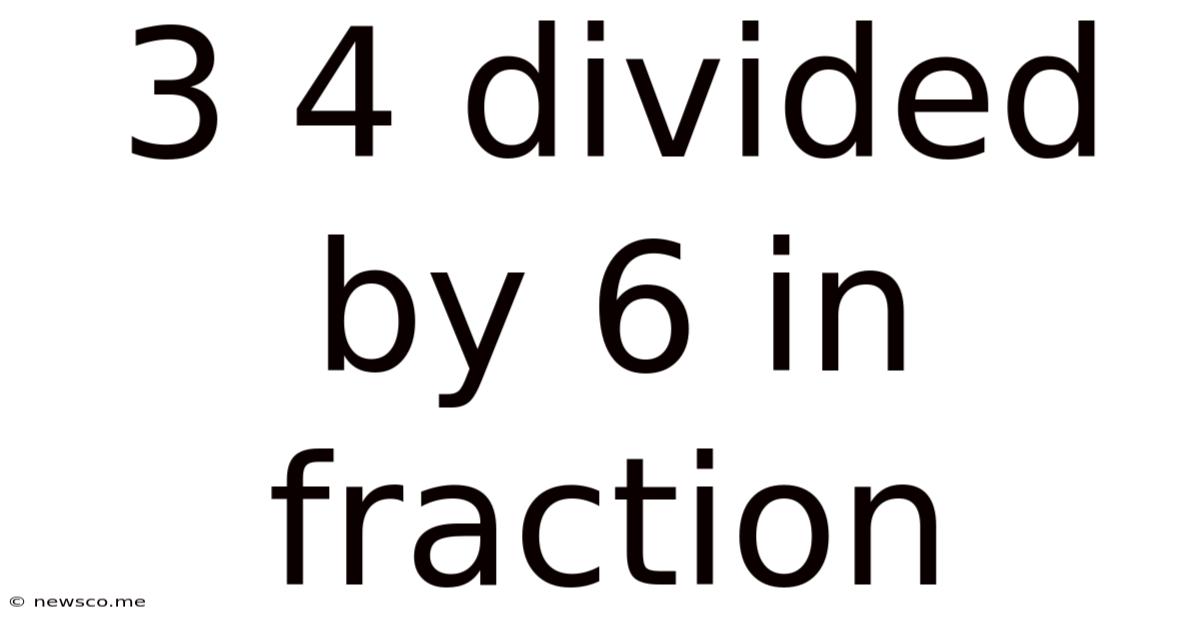
Table of Contents
3/4 Divided by 6: A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This article delves into the specifics of dividing the fraction 3/4 by the whole number 6, providing a step-by-step solution, explanations of the underlying principles, and practical examples to solidify your understanding. We'll also explore related concepts and offer tips for mastering fraction division.
Understanding Fraction Division
Before tackling the specific problem of 3/4 divided by 6, let's establish a firm grasp of the fundamental principles of fraction division. The core concept revolves around the reciprocal.
What is a Reciprocal?
The reciprocal of a number is simply 1 divided by that number. For example:
- The reciprocal of 2 is 1/2.
- The reciprocal of 5 is 1/5.
- The reciprocal of 3/4 is 4/3.
Notice that to find the reciprocal of a fraction, you switch the numerator and the denominator.
The Rule for Dividing Fractions
The golden rule for dividing fractions is: To divide by a fraction, multiply by its reciprocal. This rule simplifies the process considerably.
Let's illustrate with a simple example: 1/2 divided by 1/4. Following the rule:
1/2 ÷ 1/4 = 1/2 * 4/1 = 4/2 = 2
Solving 3/4 Divided by 6
Now, let's apply this knowledge to our specific problem: 3/4 divided by 6. Remember, 6 can be written as the fraction 6/1. Therefore, our problem becomes:
3/4 ÷ 6/1
Following the rule of multiplying by the reciprocal:
3/4 ÷ 6/1 = 3/4 * 1/6
Now we multiply the numerators together and the denominators together:
(3 * 1) / (4 * 6) = 3/24
Simplifying the Fraction
The fraction 3/24 can be simplified by finding the greatest common divisor (GCD) of the numerator (3) and the denominator (24). The GCD of 3 and 24 is 3. We divide both the numerator and the denominator by 3:
3/24 = (3 ÷ 3) / (24 ÷ 3) = 1/8
Therefore, 3/4 divided by 6 is equal to 1/8.
Visualizing the Problem
Imagine you have a pizza cut into four slices (representing 3/4 of the pizza). You need to divide this 3/4 of a pizza amongst 6 people. Each person will receive a very small slice, representing 1/8 of the whole pizza.
Practical Applications
Understanding fraction division is crucial in many real-world scenarios:
- Baking: Scaling down recipes often involves dividing fractions.
- Sewing: Calculating fabric needs often requires dividing fractions.
- Construction: Precise measurements frequently involve fractions.
- Engineering: Numerous engineering calculations rely on manipulating fractions.
Further Exploration: Dividing Fractions with Mixed Numbers
Let's extend our understanding to encompass mixed numbers. A mixed number combines a whole number and a fraction (e.g., 1 1/2). To divide fractions involving mixed numbers, you must first convert the mixed numbers into improper fractions.
Example: Divide 1 1/2 by 2/3.
-
Convert to improper fractions: 1 1/2 = (1 * 2 + 1) / 2 = 3/2
-
Apply the division rule: 3/2 ÷ 2/3 = 3/2 * 3/2 = 9/4
-
Simplify or convert back to a mixed number: 9/4 = 2 1/4
Common Mistakes to Avoid
- Forgetting the reciprocal: This is the most common mistake. Remember to always multiply by the reciprocal of the divisor.
- Incorrect simplification: Make sure you find the greatest common divisor to simplify the fraction to its lowest terms.
- Improper conversion of mixed numbers: Ensure accurate conversion of mixed numbers to improper fractions before performing division.
Mastering Fraction Division: Tips and Tricks
- Practice regularly: The more you practice, the more comfortable you'll become with the process.
- Use visual aids: Diagrams and real-world examples can help solidify your understanding.
- Break down complex problems: Tackle complex problems step-by-step.
- Check your work: Always double-check your calculations to ensure accuracy.
- Utilize online resources: Numerous websites and apps offer interactive exercises and explanations.
Conclusion
Dividing fractions, even seemingly complex ones like 3/4 divided by 6, is a manageable process once you grasp the fundamental principles. By consistently applying the rule of multiplying by the reciprocal and remembering to simplify your answers, you can confidently tackle any fraction division problem. Remember to practice regularly and utilize helpful resources to solidify your understanding and build your confidence in working with fractions. This mastery will serve you well in various academic and practical applications. Through consistent effort and the application of the techniques outlined in this guide, you can become proficient in fraction division and confidently approach similar mathematical challenges in the future.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 6 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.