3 : 4 :: X : 8
News Co
Apr 06, 2025 · 5 min read
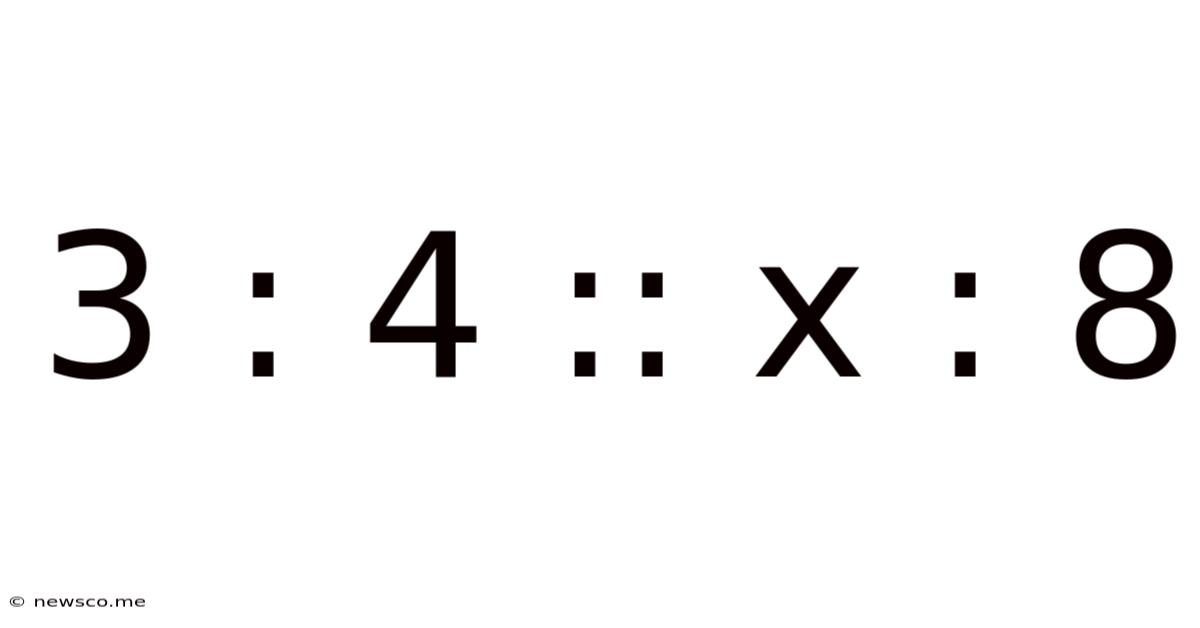
Table of Contents
Solving the Proportion: 3 : 4 :: x : 8 – A Deep Dive into Ratios and Proportions
This seemingly simple equation, 3 : 4 :: x : 8, opens the door to a fascinating world of ratios and proportions. Understanding how to solve this, and similar problems, is fundamental to various fields, from basic mathematics and everyday calculations to advanced engineering and scientific research. This article will not only solve the equation but also delve into the underlying concepts, offering a comprehensive guide for anyone looking to master ratios and proportions.
Understanding Ratios and Proportions
Before tackling the problem directly, let's solidify our understanding of the core concepts: ratios and proportions.
What is a Ratio?
A ratio is a mathematical comparison of two or more numbers. It shows the relative sizes of the numbers. We often express ratios using a colon (:) or as a fraction. For instance, the ratio of apples to oranges if you have 3 apples and 4 oranges can be written as 3:4 or 3/4. This indicates that for every 3 apples, there are 4 oranges.
What is a Proportion?
A proportion is a statement that two ratios are equal. It's essentially an equation involving ratios. The example we're dealing with, 3 : 4 :: x : 8, is a proportion. The double colon (::) signifies "is proportional to." It means that the ratio 3:4 is equal to the ratio x:8.
Solving the Proportion: 3 : 4 :: x : 8
There are several methods to solve this proportion. Let's explore the most common and effective approaches:
Method 1: Cross-Multiplication
This is arguably the most straightforward method. Cross-multiplication involves multiplying the numerator of one ratio by the denominator of the other and vice-versa, setting the products equal to each other.
-
Set up the equation: Write the proportion as an equation: 3/4 = x/8
-
Cross-multiply: Multiply 3 by 8 and 4 by x: 3 * 8 = 4 * x
-
Simplify: This gives us 24 = 4x
-
Solve for x: Divide both sides by 4: x = 24/4 = 6
Therefore, the solution to the proportion 3 : 4 :: x : 8 is x = 6.
Method 2: Scaling Up/Down
This method involves recognizing the relationship between the known values and scaling them proportionally to find the unknown value.
-
Observe the relationship: We see that the ratio 4 to 8 involves multiplying 4 by 2 (4 * 2 = 8).
-
Apply the scaling: To maintain proportionality, we must also multiply the 3 by 2: 3 * 2 = 6
-
Solution: Therefore, x = 6.
This method is particularly intuitive and efficient when the relationship between the numbers is simple and easily discernible.
Extending the Concept: More Complex Proportions
While the initial problem was relatively straightforward, the principles extend to more complex scenarios. Let's consider some variations:
Dealing with Decimal Numbers
Suppose the proportion is 2.5 : 5 :: x : 10. The methods remain the same:
-
Cross-multiplication: 2.5 * 10 = 5 * x => 25 = 5x => x = 5
-
Scaling: Notice that 5 is multiplied by 2 to get 10. Therefore, 2.5 * 2 = 5, giving us x = 5.
Incorporating Variables
Proportions can also involve other variables. For example:
2a : 3b :: 4a : x
To solve this, we need more information, such as a relationship between 'a' and 'b'. However, the cross-multiplication method would still be applied:
2a * x = 3b * 4a
Solving for x gives us: x = (12ab) / (2a) = 6b. The solution depends on the value of 'b'.
Real-World Applications of Ratios and Proportions
Ratios and proportions are not merely abstract mathematical concepts; they are integral to numerous real-world applications:
-
Scaling Recipes: If a recipe calls for 2 cups of flour and 1 cup of sugar, and you want to double the recipe, you'd use a proportion to determine the new quantities of flour and sugar.
-
Map Scales: Maps use ratios to represent distances on the ground. A scale of 1:100,000 means that 1cm on the map represents 100,000 cm (1km) on the ground.
-
Engineering and Architecture: Engineers and architects use proportions extensively in designing structures, ensuring that elements are sized appropriately and in the correct proportions.
-
Financial Calculations: Interest calculations, currency conversions, and many other financial computations rely on proportional reasoning.
-
Scientific Experiments: Researchers often use proportions to analyze data and draw conclusions from experiments.
Advanced Concepts Related to Ratios and Proportions
To further broaden your understanding, let's touch upon more advanced ideas connected to ratios and proportions:
Continued Proportions
These involve more than two ratios. For instance, a : b :: b : c represents a continued proportion. This indicates that the ratio between 'a' and 'b' is the same as the ratio between 'b' and 'c'.
Geometric Mean
The geometric mean is the central value in a continued proportion. In the example above, 'b' is the geometric mean of 'a' and 'c'.
Golden Ratio
A particularly famous ratio is the golden ratio (approximately 1.618), which appears frequently in nature and art. It's often represented by the Greek letter phi (Φ).
Troubleshooting Common Mistakes
When working with ratios and proportions, be mindful of these common pitfalls:
-
Incorrect Cross-Multiplication: Double-check your multiplication steps to avoid simple arithmetic errors.
-
Mixing Units: Ensure that all units are consistent. If you're dealing with measurements, convert them to the same units before performing calculations.
-
Misinterpreting the Proportion: Carefully examine the wording of the problem to ensure that you correctly understand which quantities are being compared.
Conclusion: Mastering Ratios and Proportions
Solving 3 : 4 :: x : 8, and understanding the broader concepts of ratios and proportions, is essential for numerous mathematical and real-world applications. By mastering cross-multiplication, scaling methods, and understanding the underlying principles, you can confidently tackle a wide range of problems involving ratios and proportions. Remember to practice consistently, exploring various examples and problem types to solidify your understanding. The ability to work with ratios and proportions is a valuable skill that will serve you well in various aspects of life and your academic or professional pursuits. So keep practicing, keep learning, and you'll find yourself navigating these concepts with ease and confidence.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 : 4 :: X : 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.