3/5 + 2/3 As A Fraction
News Co
Mar 24, 2025 · 4 min read
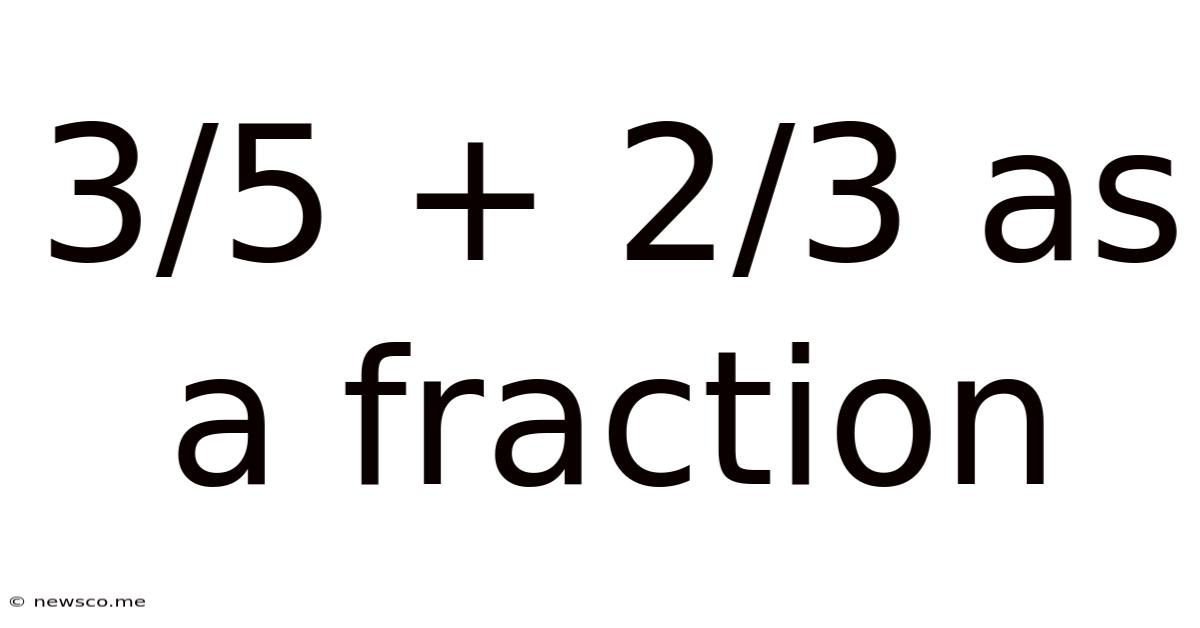
Table of Contents
3/5 + 2/3 as a Fraction: A Comprehensive Guide
Adding fractions might seem straightforward, but mastering the technique is crucial for various mathematical applications. This comprehensive guide will delve into the process of adding 3/5 and 2/3, explaining the underlying principles and providing practical examples to solidify your understanding. We'll explore different methods, address common pitfalls, and even touch upon the broader implications of fraction addition in more advanced mathematical contexts.
Understanding Fractions
Before tackling the addition of 3/5 and 2/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, representing the number of parts we have.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into.
For example, in the fraction 3/5, 3 is the numerator (the number of parts we have) and 5 is the denominator (the total number of equal parts).
Finding a Common Denominator: The Key to Fraction Addition
The fundamental rule for adding fractions is that they must share a common denominator. This means the bottom numbers (denominators) must be the same before we can add the numerators. If the denominators are different, we need to find a common denominator—a number that is a multiple of both denominators.
In our example, 3/5 + 2/3, the denominators are 5 and 3. To find a common denominator, we look for the least common multiple (LCM) of 5 and 3. Since 5 and 3 are prime numbers, their LCM is simply their product: 5 x 3 = 15.
Converting Fractions to a Common Denominator
Now that we have a common denominator of 15, we need to convert both fractions (3/5 and 2/3) so they have this denominator. We do this by multiplying both the numerator and the denominator of each fraction by the appropriate factor.
-
For 3/5: To get a denominator of 15, we need to multiply the denominator (5) by 3. To maintain the value of the fraction, we must also multiply the numerator (3) by 3: (3 x 3) / (5 x 3) = 9/15
-
For 2/3: To get a denominator of 15, we need to multiply the denominator (3) by 5. Again, we must also multiply the numerator (2) by 5: (2 x 5) / (3 x 5) = 10/15
Adding the Fractions
With both fractions now having a common denominator of 15, we can finally add them:
9/15 + 10/15 = (9 + 10) / 15 = 19/15
Simplifying the Result
The result, 19/15, is an improper fraction (where the numerator is larger than the denominator). We can simplify this by converting it to a mixed number. To do this, we divide the numerator (19) by the denominator (15):
19 ÷ 15 = 1 with a remainder of 4
This means 19/15 is equal to 1 and 4/15. Therefore:
3/5 + 2/3 = 19/15 = 1 4/15
Alternative Methods: Using the Least Common Multiple (LCM) Directly
While the step-by-step method is clear, understanding the LCM directly can streamline the process. Remember that the LCM of 5 and 3 is 15. We can express the fractions with this denominator directly:
- 3/5 becomes (3/5) * (3/3) = 9/15
- 2/3 becomes (2/3) * (5/5) = 10/15
Adding these gives us 9/15 + 10/15 = 19/15, which simplifies to 1 4/15, as before.
Practical Applications of Fraction Addition
Adding fractions is a fundamental skill with numerous applications in various fields:
- Baking and Cooking: Adjusting recipes, scaling ingredients, and understanding portion sizes often involve fraction addition.
- Construction and Engineering: Precise measurements and calculations in construction and engineering often utilize fractions.
- Finance and Accounting: Calculating portions of investments, interest rates, and budgets frequently involves fractions.
- Science and Physics: Representing quantities and proportions in scientific experiments and formulas often relies on fractions.
Troubleshooting Common Mistakes
- Forgetting to find a common denominator: This is the most common mistake. Remember, you cannot add fractions with different denominators directly.
- Incorrectly converting fractions: Always multiply both the numerator and denominator by the same factor when changing the denominator.
- Simplifying errors: Make sure to simplify the resulting fraction to its lowest terms if possible.
Advanced Concepts: Adding More Than Two Fractions
The same principles apply when adding more than two fractions. Find the LCM of all the denominators and convert each fraction to the common denominator before adding the numerators.
For example, let's add 1/2 + 1/3 + 1/4:
The LCM of 2, 3, and 4 is 12.
- 1/2 becomes 6/12
- 1/3 becomes 4/12
- 1/4 becomes 3/12
Adding them: 6/12 + 4/12 + 3/12 = 13/12 = 1 1/12
Conclusion: Mastering Fraction Addition
Adding fractions, while seemingly simple, requires a solid understanding of fundamental concepts like common denominators and simplifying fractions. Mastering this skill forms a crucial foundation for more advanced mathematical concepts and finds widespread applications in various real-world scenarios. By consistently practicing and understanding the underlying principles, you can build confidence and efficiency in tackling any fraction addition problem. Remember the key steps: find a common denominator, convert fractions, add numerators, and simplify the result. With these techniques, you’ll confidently solve fraction addition problems and seamlessly integrate this skill into other mathematical pursuits.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3/5 + 2/3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.