3 7 Divided By 3 7
News Co
Apr 21, 2025 · 6 min read
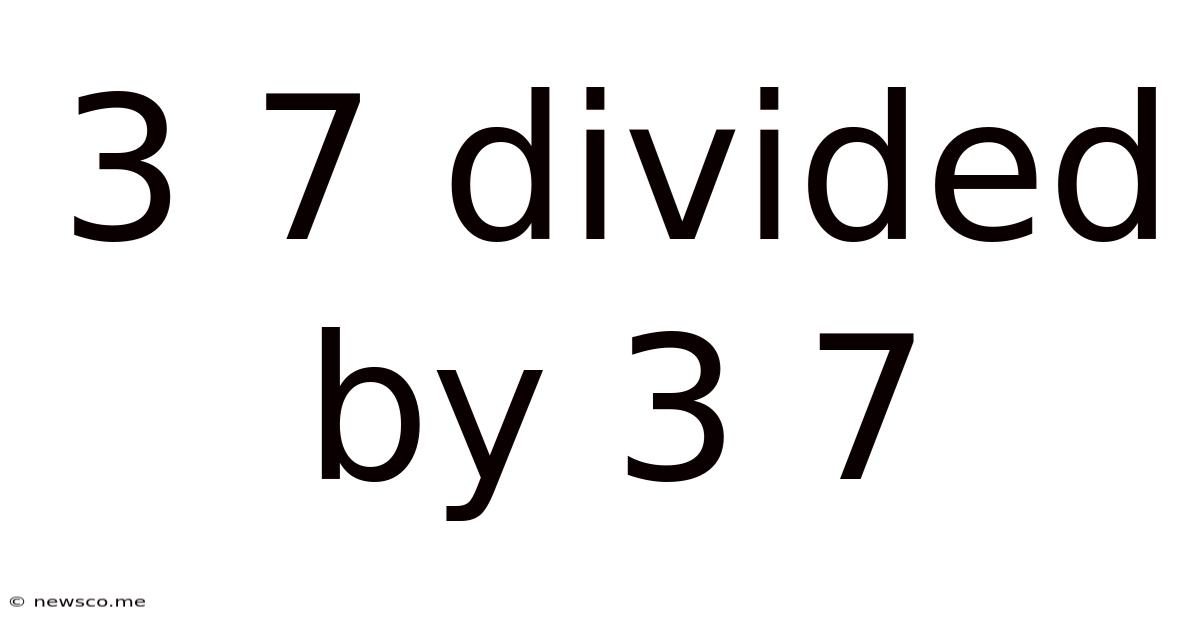
Table of Contents
Decoding the Enigma: 37 Divided by 37
The seemingly simple arithmetic problem of 37 divided by 37 might appear trivial at first glance. However, exploring this seemingly straightforward calculation opens doors to understanding fundamental mathematical concepts, their applications, and even delves into the fascinating world of numerical representation and computational processes. This article will dissect this problem, going far beyond the simple answer of '1,' to examine its implications in various mathematical contexts.
H2: The Obvious Answer and its Implications
At its core, 37 divided by 37 equals 1. This is a direct application of the division operation, where a number (the dividend, 37) is divided by another number (the divisor, 37). The result (the quotient) indicates how many times the divisor fits into the dividend. In this case, 37 fits into 37 exactly once. This seemingly basic operation forms the bedrock of numerous more complex mathematical computations.
H3: Understanding Division: A Deeper Dive
Division can be understood in multiple ways:
-
Partitioning: Dividing 37 by 37 is akin to partitioning 37 objects into groups of 37. This results in a single group.
-
Repeated Subtraction: Division can be viewed as repeated subtraction. How many times can you subtract 37 from 37 before reaching zero? Only once.
-
Inverse of Multiplication: Division is the inverse operation of multiplication. Since 37 multiplied by 1 equals 37, then 37 divided by 37 must equal 1. This inverse relationship is crucial in algebra and solving equations.
H2: Expanding the Scope: Beyond the Simple Calculation
While the answer to 37 divided by 37 is undeniably 1, the problem's simplicity allows us to explore related concepts and their wider applications:
H3: The Concept of Identity in Mathematics
The number 1 holds a unique position in mathematics. It's the multiplicative identity, meaning that any number multiplied by 1 remains unchanged. The result of 37 divided by 37 reinforces this concept. It shows that dividing a number by itself results in the multiplicative identity, 1. This principle is fundamental in various mathematical fields.
H3: Applications in Real-World Scenarios
Although seemingly abstract, the concept of dividing a number by itself has practical applications. Consider these scenarios:
-
Unit Pricing: If you buy a single item costing 37 dollars, the unit price is calculated by dividing the total cost (37) by the number of items (1). The calculation is essentially 37/1 = 37, but the underlying principle is the same as 37/37 = 1 – the cost of a single unit.
-
Proportion and Ratio: When comparing quantities, the concept of a ratio comes into play. If you have 37 apples and 37 oranges, the ratio of apples to oranges is 37:37, which simplifies to 1:1. This simplification hinges on the understanding that 37/37 = 1.
-
Probability: In probability calculations, determining the probability of a certain event often involves dividing the number of favorable outcomes by the total number of possible outcomes. If there's only one favorable outcome out of a total of 37 possibilities, the probability is 1/37. While this is not directly 37/37, the understanding of this fundamental division operation is crucial.
H2: Exploring Different Number Systems
The simplicity of 37/37 = 1 holds true regardless of the number system used. Whether we're working with decimal, binary, hexadecimal, or any other base, dividing a number by itself always yields the equivalent of 1 in that system. This highlights the fundamental nature of the division operation and its consistency across different mathematical representations.
H3: Binary Representation
In binary (base-2), 37 is represented as 100101. While the calculation itself wouldn't be visually identical to the decimal calculation, the underlying concept remains the same. Dividing the binary representation of 37 by itself would result in the binary representation of 1 (which is simply 1).
H3: Hexadecimal Representation
Similarly, in hexadecimal (base-16), 37 is represented as 25. Again, the calculation would look different, but the result would still be the equivalent of 1 in the hexadecimal system. This consistency underscores the universality of the mathematical principle.
H2: Computational Considerations
The simplicity of this calculation belies the complexity of how computers perform division. Even seemingly straightforward calculations involve intricate processes within a computer's central processing unit (CPU).
H3: Integer Division vs. Floating-Point Division
Computers distinguish between integer division (division of whole numbers) and floating-point division (division involving decimal numbers). In the case of 37/37, the result would be the same regardless of whether integer or floating-point division is used, yielding a precise 1. However, with other division problems, the differences become significant. For example, the result of 37/3 (integer division) would be 12, while the result of 37/3 (floating-point division) would be approximately 12.333.
H3: Computational Efficiency
Although 37/37 is a trivial calculation for a modern computer, the efficiency of division algorithms becomes crucial when dealing with very large numbers or complex computations. The optimization of division algorithms is an ongoing area of research in computer science, influencing the speed and performance of various software applications and scientific simulations.
H2: Extending the Concept: Dividing by Zero
While 37 divided by 37 is well-defined and straightforward, the question of dividing by zero is a fundamentally different issue. Dividing by zero is undefined in mathematics. This is because division can be interpreted as the inverse of multiplication. There is no number that, when multiplied by zero, results in 37 (or any other non-zero number). Attempting to divide by zero leads to inconsistencies and paradoxes within the mathematical system.
H2: Applications in Advanced Mathematics
While the simple division 37/37 might seem elementary, the underlying principles extend to far more advanced areas of mathematics.
H3: Abstract Algebra
In abstract algebra, the concept of an identity element is a central theme. The number 1 in the context of multiplication serves as the identity element. The result of 37/37 reinforces the importance of identity elements in various algebraic structures.
H3: Number Theory
Number theory deals with the properties of numbers, including divisibility. The fact that 37 is divisible by itself highlights the basic concepts of divisibility which are foundational to many aspects of number theory.
H3: Calculus and Analysis
While not directly relevant to the 37/37 problem itself, the fundamental concepts of limits and continuity in calculus rely heavily on division and the notion of approaching values infinitely close to zero, highlighting the important distinctions between dividing by a very small number and dividing by zero itself.
H2: Conclusion: The Significance of Simplicity
The seemingly insignificant problem of 37 divided by 37 provides a rich foundation for exploring core mathematical concepts, their applications in various fields, and even the intricate workings of computational processes. It highlights the power of seemingly simple operations and their influence on more complex mathematical ideas. The simplicity of the answer, 1, should not overshadow the depth of understanding that can be gained by exploring the problem's implications across different branches of mathematics and computer science. This elementary calculation serves as a powerful reminder that even the most fundamental mathematical principles hold immense significance and widespread applicability. By exploring such seemingly straightforward problems, we can foster a deeper appreciation for the beauty and elegance of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 7 Divided By 3 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.