3 8 Divided By 2 In Fraction
News Co
May 07, 2025 · 5 min read
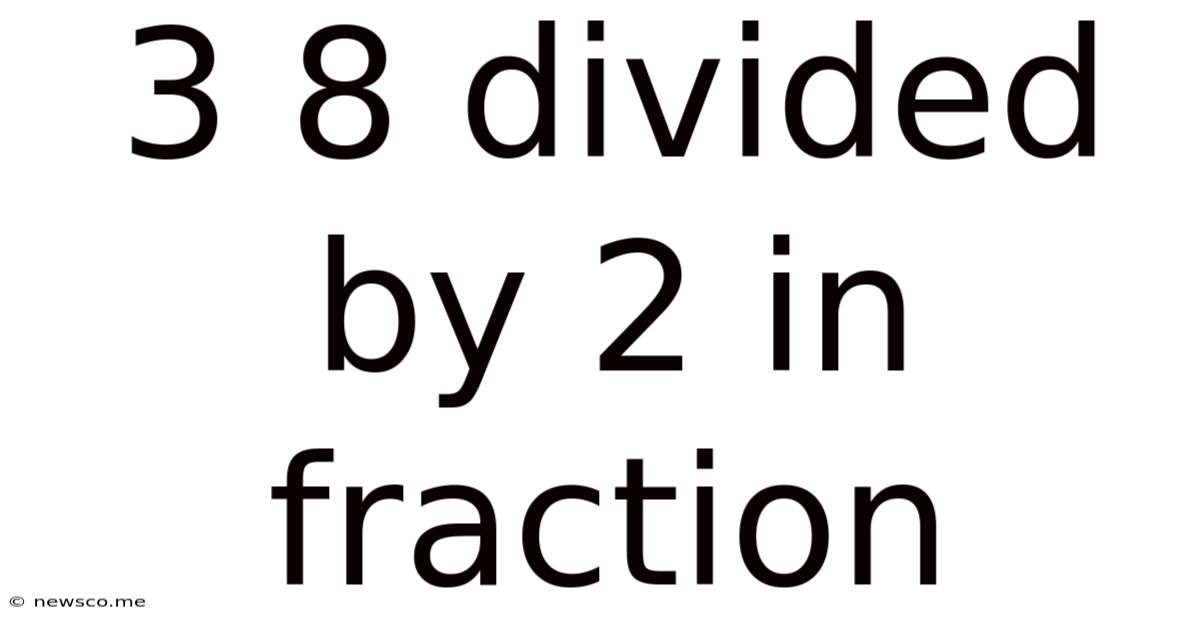
Table of Contents
- 3 8 Divided By 2 In Fraction
- Table of Contents
- 3 8/2: A Deep Dive into Fraction Division
- Understanding the Components: Mixed Numbers and Improper Fractions
- Converting Mixed Numbers to Improper Fractions
- Methods for Dividing Fractions
- Method 1: The Reciprocal Method
- Alternative Approach: Focusing on Whole Numbers and Fractions Separately
- Practical Applications and Real-World Examples
- Troubleshooting Common Mistakes
- Mastering Fraction Division: Tips and Practice
- Conclusion: Embracing the Power of Fraction Division
- Latest Posts
- Related Post
3 8/2: A Deep Dive into Fraction Division
Understanding fraction division, particularly mixed numbers like 3 8/2, can seem daunting at first. However, with a systematic approach and a solid grasp of the underlying principles, solving these problems becomes straightforward and even intuitive. This article will guide you through the process of dividing 3 8/2, exploring the various methods, explaining the reasoning behind them, and offering practical tips for mastering fraction division in general.
Understanding the Components: Mixed Numbers and Improper Fractions
Before diving into the division itself, let's clarify the components of our problem: 3 8/2. This is a mixed number, combining a whole number (3) and a fraction (8/2). To perform division with mixed numbers, it's often easier to convert them into improper fractions.
Converting Mixed Numbers to Improper Fractions
An improper fraction has a numerator larger than its denominator. To convert a mixed number to an improper fraction, follow these steps:
- Multiply the whole number by the denominator: In our example, 3 (whole number) x 2 (denominator) = 6.
- Add the numerator: 6 + 8 (numerator) = 14.
- Keep the same denominator: The denominator remains 2.
Therefore, 3 8/2 converts to the improper fraction 14/2.
Methods for Dividing Fractions
Now that we've converted our mixed number, let's explore the different methods for dividing fractions. We'll focus on the method most commonly used for simplicity and ease of understanding.
Method 1: The Reciprocal Method
The most efficient method for dividing fractions involves using reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For instance, the reciprocal of 2/3 is 3/2.
Here's how to apply this method:
-
Convert to Improper Fractions (if necessary): As we've already done, convert the mixed number 3 8/2 into the improper fraction 14/2.
-
Rewrite the division as multiplication: Instead of dividing by a fraction, we multiply by its reciprocal. So, 14/2 ÷ 2/1 becomes 14/2 x 1/2.
-
Multiply the numerators: 14 x 1 = 14.
-
Multiply the denominators: 2 x 2 = 4.
-
Simplify the result: Our initial result is 14/4. Both numerator and denominator are divisible by 2, simplifying to 7/2.
-
Convert back to a mixed number (optional): While 7/2 is perfectly acceptable, we can convert it back to a mixed number. 7 divided by 2 is 3 with a remainder of 1. Therefore, 7/2 is equivalent to 3 1/2.
Therefore, 3 8/2 divided by 2/1 = 3 1/2.
Alternative Approach: Focusing on Whole Numbers and Fractions Separately
An alternative approach involves tackling the whole number and fractional parts separately. While less efficient in many cases, understanding this method can reinforce the foundational concepts.
First, we separate our mixed number into its components: 3 + 8/2. This can be rewritten as:
(3 + 8/2) ÷ 2
Now, let's divide each part separately:
- Dividing the whole number: 3 ÷ 2 = 1.5 or 1 1/2
- Dividing the fraction: (8/2) ÷ 2 = 8/2 x 1/2 = 8/4 = 2
Adding these results gives: 1.5 + 2 = 3.5 or 3 1/2.
This method highlights that dividing a mixed number involves dividing each part individually and then combining the results. However, it's generally more efficient to use the reciprocal method outlined above, particularly for more complex problems.
Practical Applications and Real-World Examples
Understanding fraction division extends far beyond textbook exercises. It's a crucial skill with diverse real-world applications.
Example 1: Baking: A recipe calls for 3 1/2 cups of flour, and you want to make half the recipe. You need to divide 3 1/2 by 2. This involves using fraction division to determine the correct amount of flour.
Example 2: Construction: Dividing lumber of a certain length into smaller pieces requires understanding fractions and division to ensure accurate measurements.
Example 3: Sewing: Dividing fabric to create patterns, or determining the amount of fabric needed for a particular project often involves fraction division.
Troubleshooting Common Mistakes
Several common errors can hinder the successful division of fractions. Let's address some of these:
- Forgetting to convert mixed numbers to improper fractions: Attempting to divide mixed numbers directly without converting them to improper fractions often leads to incorrect results.
- Multiplying instead of using the reciprocal: Remember, division by a fraction is equivalent to multiplication by its reciprocal. Confusing this step is a frequent source of error.
- Incorrect simplification: Ensure your final answer is simplified to its lowest terms. Failure to simplify can lead to an answer that is mathematically correct but not presented in its most concise form.
Mastering Fraction Division: Tips and Practice
The key to mastering fraction division lies in consistent practice and a clear understanding of the fundamental principles. Here are some helpful tips:
- Start with simpler examples: Begin with easy problems to build confidence and familiarity with the process.
- Use visual aids: Diagrams and visual representations can help to conceptualize fraction division, especially for beginners.
- Practice regularly: Consistent practice is essential for solidifying your understanding and improving your speed and accuracy.
- Seek help when needed: Don't hesitate to ask for help from teachers, tutors, or online resources if you encounter difficulties.
- Work through diverse problem sets: Engage with a variety of problems, including those with mixed numbers, improper fractions, and different denominators.
Conclusion: Embracing the Power of Fraction Division
Fraction division, while initially challenging, becomes a manageable and even enjoyable skill with consistent practice and a clear understanding of the methods involved. The reciprocal method, combined with the ability to convert between mixed numbers and improper fractions, provides a powerful toolkit for tackling any fraction division problem. Remember to focus on accuracy, practice regularly, and celebrate your progress as you master this fundamental mathematical concept. By overcoming this hurdle, you unlock a deeper understanding of mathematical operations and broaden your capacity to solve a wide array of practical problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 8 Divided By 2 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.