3 9 27 81 Next Number
News Co
Mar 21, 2025 · 5 min read
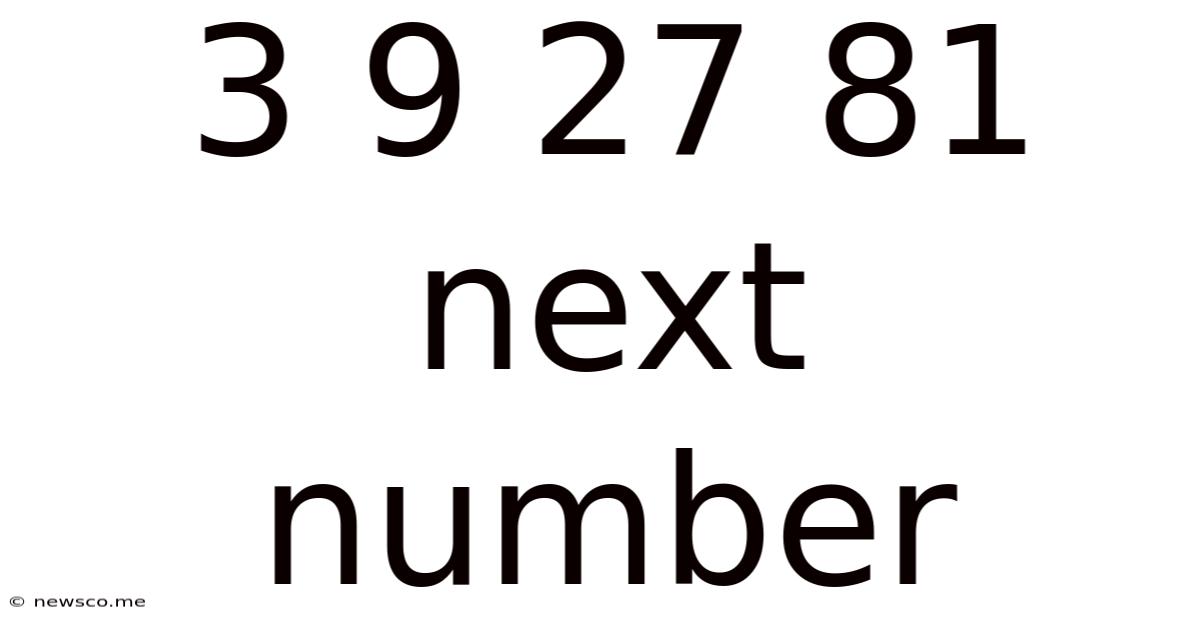
Table of Contents
3 9 27 81: Unlocking the Secrets of Number Sequences and the Next Number in the Series
The seemingly simple sequence "3, 9, 27, 81..." holds a fascinating allure for mathematicians and puzzle enthusiasts alike. At first glance, it appears straightforward, but a deeper dive reveals the underlying principles governing its progression and unlocks the key to predicting the next number and many more beyond it. This article delves into the intricacies of this numerical sequence, exploring different mathematical concepts, providing a step-by-step solution, and offering broader insights into the world of number patterns.
Understanding the Pattern: Geometric Progression
The core to solving this sequence lies in recognizing its type: a geometric progression (GP). A geometric progression is a sequence where each term is obtained by multiplying the previous term by a constant value, known as the common ratio. In our sequence, 3, 9, 27, 81, this constant ratio is easily identifiable.
Calculating the Common Ratio
Let's examine the relationship between consecutive terms:
- 9 / 3 = 3
- 27 / 9 = 3
- 81 / 27 = 3
The common ratio is consistently 3. This confirms that we are dealing with a geometric progression.
Finding the Next Number: Applying the Common Ratio
Now that we've identified the common ratio, predicting the next number becomes a simple matter of multiplication. To find the next term in the sequence, we multiply the last term (81) by the common ratio (3):
81 * 3 = 243
Therefore, the next number in the sequence 3, 9, 27, 81 is 243.
Extending the Sequence: Exploring Further Terms
The beauty of understanding the underlying pattern allows us to extend the sequence indefinitely. By continuing to multiply by the common ratio, we can generate numerous subsequent terms. For example:
- 243 * 3 = 729
- 729 * 3 = 2187
- 2187 * 3 = 6561
- and so on...
This simple multiplication process reveals the power of identifying patterns in mathematics.
Beyond the Basics: Exploring Variations and Extensions
While the core concept is straightforward, let's explore some interesting variations and extensions related to this sequence:
1. The Formula for a Geometric Progression
The nth term of a geometric progression can be calculated using the formula:
a<sub>n</sub> = a<sub>1</sub> * r<sup>(n-1)</sup>
Where:
- a<sub>n</sub> is the nth term of the sequence
- a<sub>1</sub> is the first term of the sequence
- r is the common ratio
- n is the term number
Applying this to our sequence:
If we want to find the 10th term (n=10), a<sub>1</sub> = 3, and r = 3:
a<sub>10</sub> = 3 * 3<sup>(10-1)</sup> = 3 * 3<sup>9</sup> = 19683
2. Sum of a Geometric Progression
We can also calculate the sum of the first 'n' terms of a geometric progression using the formula:
S<sub>n</sub> = a<sub>1</sub> * (1 - r<sup>n</sup>) / (1 - r)
For instance, the sum of the first 5 terms of our sequence (3, 9, 27, 81, 243) would be:
S<sub>5</sub> = 3 * (1 - 3<sup>5</sup>) / (1 - 3) = 3 * (1 - 243) / (-2) = 363
3. Sequences with Different Starting Points and Ratios
The principle of geometric progression applies to countless other number sequences. Consider these examples:
- Sequence: 2, 6, 18, 54... (Common ratio: 3)
- Sequence: 5, 10, 20, 40... (Common ratio: 2)
- Sequence: 1, 1/2, 1/4, 1/8... (Common ratio: 1/2)
These examples demonstrate the versatility and widespread application of the geometric progression concept.
4. Real-World Applications of Geometric Progressions
Geometric progressions are far from being just abstract mathematical concepts. They find practical applications in various fields, including:
- Finance: Compound interest calculations rely on geometric progressions to model the growth of investments over time.
- Biology: Population growth in ideal conditions can often be modeled using geometric progressions.
- Physics: Radioactive decay follows a geometric progression, with the amount of radioactive material decreasing by a constant factor over time.
- Computer Science: Certain algorithms and data structures utilize geometric progressions for efficiency and scalability.
Problem Solving Strategies and Critical Thinking
Solving number sequences like "3, 9, 27, 81..." involves more than just applying formulas; it's about developing crucial problem-solving skills:
- Pattern Recognition: The ability to identify underlying patterns is paramount. This requires careful observation and analysis of the relationships between numbers.
- Deductive Reasoning: Based on observed patterns, you need to deduce the rules governing the sequence. This involves logical inference and eliminating possibilities.
- Mathematical Knowledge: A foundational understanding of mathematical concepts like geometric progressions, arithmetic progressions, and other number series is essential.
- Verification: Once you've identified a pattern and predicted the next number, it's crucial to verify your solution by checking its consistency with the established pattern.
Conclusion: Embracing the Power of Patterns
The seemingly simple sequence "3, 9, 27, 81..." provides a gateway to understanding the power and elegance of mathematical patterns. By recognizing its underlying geometric progression, we've not only determined the next number (243) but also gained insights into broader mathematical principles and their applications in various fields. This exercise highlights the importance of pattern recognition, critical thinking, and the application of mathematical knowledge in solving problems and unlocking the secrets hidden within seemingly simple numerical sequences. The ability to identify and extrapolate these patterns extends far beyond simple number puzzles, empowering us to analyze and understand complex systems in various areas of life and science. Remember, the key to success lies in careful observation, logical deduction, and a solid grasp of fundamental mathematical concepts.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 3 9 27 81 Next Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.