3 Divided By 3 7 In Fraction
News Co
Apr 27, 2025 · 4 min read
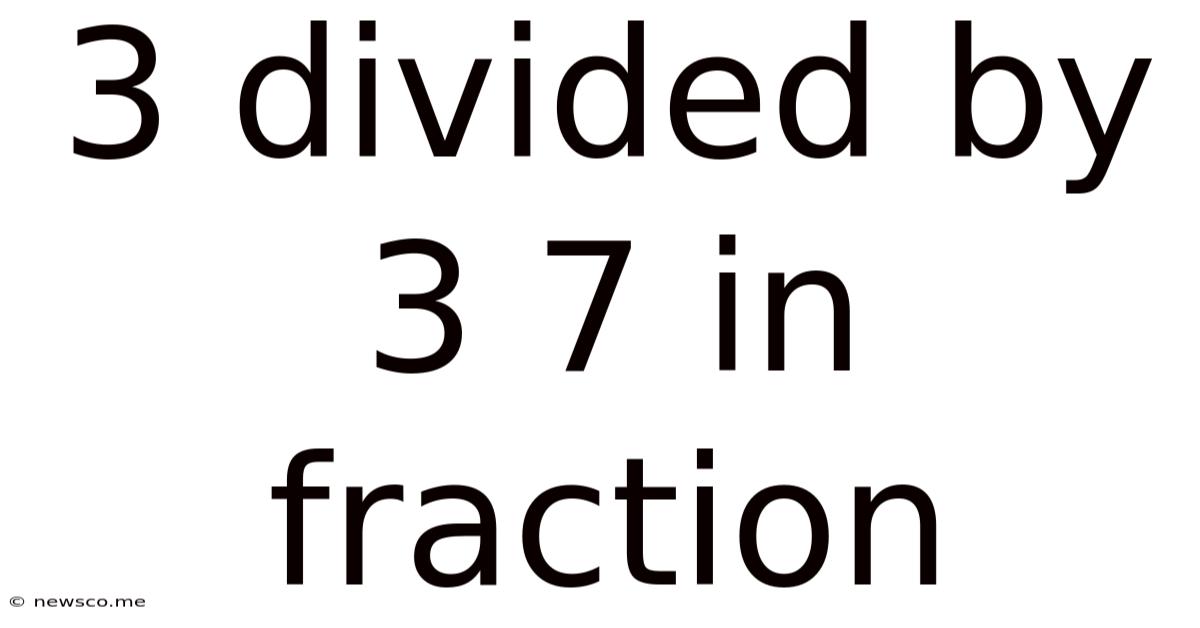
Table of Contents
3 Divided by 3/7: A Comprehensive Guide to Fraction Division
Understanding fraction division can be tricky, but mastering it unlocks a world of mathematical possibilities. This comprehensive guide will delve into the intricacies of dividing 3 by 3/7, explaining the process step-by-step, offering various approaches, and exploring the underlying mathematical principles. We'll also examine practical applications and provide further examples to solidify your understanding.
Understanding the Problem: 3 ÷ 3/7
The problem "3 divided by 3/7" can be written as:
3 ÷ 3/7
This represents the question: "How many times does 3/7 fit into 3?" This might seem counterintuitive at first, dealing with fractions within a whole number, but using the right techniques will make the solution clear.
Method 1: The Reciprocal Method
This is the most common and efficient method for dividing fractions. The core principle is to change the division problem into a multiplication problem by using the reciprocal of the second fraction.
Step 1: Find the reciprocal of the divisor.
The divisor is the fraction you're dividing by, which is 3/7. The reciprocal of a fraction is found by swapping the numerator and the denominator. The reciprocal of 3/7 is therefore 7/3.
Step 2: Change division to multiplication.
Rewrite the problem as a multiplication problem:
3 x 7/3
Step 3: Simplify and solve.
Now, you can multiply the whole number (3) by the numerator (7) of the fraction:
3 x 7 = 21
The denominator remains the same:
21/3
Finally, simplify the resulting fraction:
21/3 = 7
Therefore, 3 divided by 3/7 equals 7.
Method 2: Visual Representation
While less efficient for complex problems, visualizing the division can help solidify understanding, especially for beginners.
Imagine you have 3 whole units. Each unit needs to be divided into portions of 3/7. To do this, you would first divide each whole unit into seven equal sections. This creates a total of 3 x 7 = 21 sections. Since each portion you're looking for is 3/7, you would group the sections into sets of 3.
How many sets of 3 sections are there? There are 21 sections total divided into sets of 3, so there are 21/3 = 7 sets. Again, this visually demonstrates that 3 divided by 3/7 equals 7.
Method 3: Converting to Improper Fractions
This method involves converting the whole number into an improper fraction before performing the division.
Step 1: Convert the whole number to an improper fraction.
The whole number 3 can be represented as 3/1.
Step 2: Perform fraction division.
Now, the problem becomes:
(3/1) ÷ (3/7)
Remember the rule for dividing fractions: keep the first fraction the same, change the division sign to multiplication, and flip the second fraction (find its reciprocal):
(3/1) x (7/3)
Step 3: Simplify and solve.
Multiply the numerators together and the denominators together:
(3 x 7) / (1 x 3) = 21/3
Simplify the fraction:
21/3 = 7
Once again, we arrive at the solution: 7.
Practical Applications
Understanding fraction division has widespread practical applications:
- Cooking and Baking: Scaling recipes up or down requires dividing and multiplying fractions. For example, if a recipe calls for 3/7 cup of flour and you want to triple the recipe, you need to calculate 3 x (3/7).
- Sewing and Tailoring: Calculating fabric requirements for garments often involves fraction division.
- Construction and Engineering: Precise measurements in construction and engineering frequently involve fractions, necessitating accurate division.
- Data Analysis: When working with datasets, you may need to divide fractional data points.
- Financial Calculations: Proportionate distribution of resources or profits often involves fraction division.
Further Examples
Let's solidify our understanding with a few more examples:
- 5 ÷ 2/5: The reciprocal of 2/5 is 5/2. 5 x 5/2 = 25/2 = 12.5
- 1/2 ÷ 1/4: The reciprocal of 1/4 is 4/1. 1/2 x 4/1 = 4/2 = 2
- 7/8 ÷ 1/16: The reciprocal of 1/16 is 16/1. 7/8 x 16/1 = 112/8 = 14
These examples demonstrate the consistent application of the reciprocal method for solving fraction division problems.
Conclusion: Mastering Fraction Division
Dividing by fractions, particularly a problem like 3 divided by 3/7, might seem daunting initially. However, by understanding the underlying principles and employing the appropriate methods – whether it's the reciprocal method, visual representation, or converting to improper fractions – solving such problems becomes straightforward. This guide has provided a comprehensive exploration of these techniques, along with practical applications and further examples to reinforce your understanding. With practice, you'll confidently tackle fraction division in various contexts. Remember, the key is to master the concept of the reciprocal and apply it consistently to transform division problems into simpler multiplication problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 Divided By 3 7 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.