3 Equivalent Fractions For 1 2
News Co
Mar 21, 2025 · 5 min read
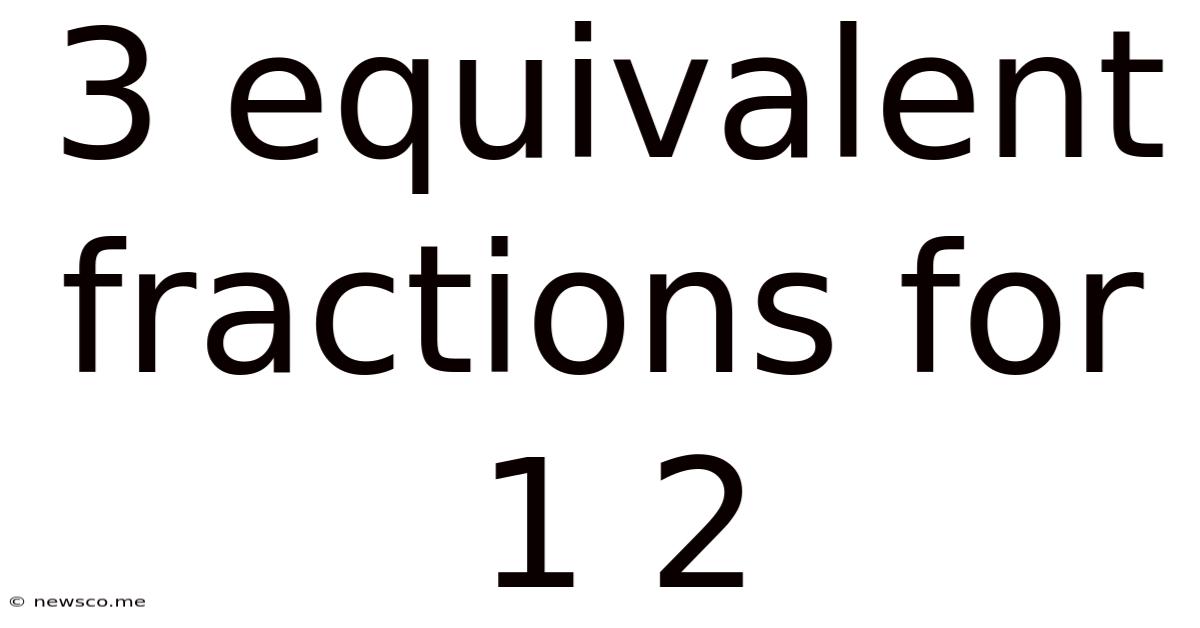
Table of Contents
3 Equivalent Fractions for 1 ½: A Deep Dive into Fraction Equivalence
Understanding fractions is a cornerstone of mathematical literacy. While seemingly simple, mastering the concept of equivalent fractions unlocks a deeper understanding of numbers and their relationships. This article explores the concept of equivalent fractions, focusing specifically on finding three equivalent fractions for the mixed number 1 ½. We'll delve into the underlying principles, provide practical examples, and explore various methods for finding equivalent fractions. By the end, you'll not only know three equivalent fractions for 1 ½ but also possess the skills to find equivalent fractions for any given fraction.
What are Equivalent Fractions?
Equivalent fractions represent the same portion of a whole, even though they look different. Think of cutting a pizza: ½ a pizza is the same as 2/4, 3/6, 4/8, and so on. Each fraction represents the same amount of pizza, just with different-sized slices. The key is that the ratio between the numerator (the top number) and the denominator (the bottom number) remains constant. This means you can multiply or divide both the numerator and the denominator by the same non-zero number to create an equivalent fraction.
Converting Mixed Numbers to Improper Fractions
Before we find equivalent fractions for 1 ½, we need to convert this mixed number into an improper fraction. A mixed number combines a whole number and a fraction (e.g., 1 ½). An improper fraction has a numerator larger than or equal to its denominator (e.g., 3/2).
To convert 1 ½ to an improper fraction:
- Multiply the whole number by the denominator: 1 * 2 = 2
- Add the numerator: 2 + 1 = 3
- Keep the same denominator: 2
Therefore, 1 ½ is equivalent to the improper fraction ³⁄₂. This form is crucial for easily finding equivalent fractions.
Finding Three Equivalent Fractions for ³⁄₂
Now that we have our improper fraction, we can easily find equivalent fractions by multiplying both the numerator and the denominator by the same number. Let's find three equivalent fractions:
Equivalent Fraction 1: Multiplying by 2
Multiply both the numerator and the denominator of ³⁄₂ by 2:
(3 * 2) / (2 * 2) = ⁶⁄₄
Therefore, ⁶⁄₄ is an equivalent fraction to 1 ½ and ³⁄₂.
Equivalent Fraction 2: Multiplying by 3
Multiply both the numerator and the denominator of ³⁄₂ by 3:
(3 * 3) / (2 * 3) = ⁹⁄₆
Therefore, ⁹⁄₆ is another equivalent fraction to 1 ½, ³⁄₂, and ⁶⁄₄.
Equivalent Fraction 3: Multiplying by 4
Multiply both the numerator and the denominator of ³⁄₂ by 4:
(3 * 4) / (2 * 4) = ¹²⁄₈
Therefore, ¹²⁄₈ is a third equivalent fraction to 1 ½, ³⁄₂, ⁶⁄₄, and ⁹⁄₆.
Visualizing Equivalent Fractions
Visual representations can greatly aid in understanding equivalent fractions. Imagine a circle representing a whole. Dividing it into two equal parts shows ½. Dividing the same circle into four equal parts and shading two of them shows ⅔. Both represent the same amount of the circle, demonstrating their equivalence. You can extend this visualization to other equivalent fractions of 1 ½, like ⁶⁄₄, ⁹⁄₆, and ¹²⁄₈, each showing the same total area shaded.
Simplifying Fractions: The Inverse Operation
While we multiplied to find equivalent fractions, we can also simplify fractions by dividing both the numerator and the denominator by their greatest common divisor (GCD). For example, ⁶⁄₄ can be simplified to ³⁄₂ by dividing both by 2 (their GCD). This highlights the reversible nature of creating equivalent fractions: you can expand them by multiplying or reduce them by dividing.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions isn't just an abstract mathematical concept; it has numerous practical applications in everyday life and various fields:
- Cooking and Baking: Recipes often require adjusting ingredient quantities. If a recipe calls for ½ cup of sugar, but you want to double the recipe, you'll need 1 cup (which is equivalent to 2/2).
- Measurement: Converting units of measurement often involves working with equivalent fractions. For example, converting inches to feet or centimeters to meters.
- Construction and Engineering: Precise calculations are vital in these fields, and understanding equivalent fractions helps ensure accuracy in measurements and proportions.
- Finance: Dealing with percentages and ratios involves the concept of equivalent fractions. Calculating interest rates, discounts, and proportions often requires working with equivalent fractions.
- Data Analysis: Representing data visually and understanding proportions in charts and graphs relies heavily on the comprehension of equivalent fractions.
Beyond 1 ½: Finding Equivalent Fractions for Any Fraction
The methods described above can be applied to find equivalent fractions for any fraction, whether it's a proper fraction, an improper fraction, or a mixed number. The key principle remains the same: multiply or divide both the numerator and the denominator by the same non-zero number.
Troubleshooting Common Mistakes
When working with equivalent fractions, some common mistakes can occur:
- Only multiplying or dividing the numerator or denominator: Remember that both the numerator and the denominator must be multiplied or divided by the same number to maintain equivalence.
- Using zero as a multiplier or divisor: Dividing by zero is undefined, so it's crucial to avoid using zero in these calculations.
- Incorrectly simplifying fractions: Ensure you find the greatest common divisor (GCD) to simplify fractions to their lowest terms efficiently.
Conclusion: Mastering the Art of Equivalent Fractions
Mastering the concept of equivalent fractions opens up a world of mathematical possibilities. By understanding how to find and use equivalent fractions, you gain a more profound understanding of numbers, proportions, and their diverse applications in real-world scenarios. This article provided a comprehensive guide to finding three equivalent fractions for 1 ½, but the underlying principles and techniques can be applied to any fraction, empowering you to confidently tackle various mathematical challenges. Remember to practice regularly to build your skills and reinforce your understanding of this fundamental concept. The more you practice, the more intuitive and effortless finding equivalent fractions will become. So, grab a pencil and paper, and start exploring the fascinating world of fractions!
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 3 Equivalent Fractions For 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.