3 Is What Percent Of 4
News Co
Mar 24, 2025 · 5 min read
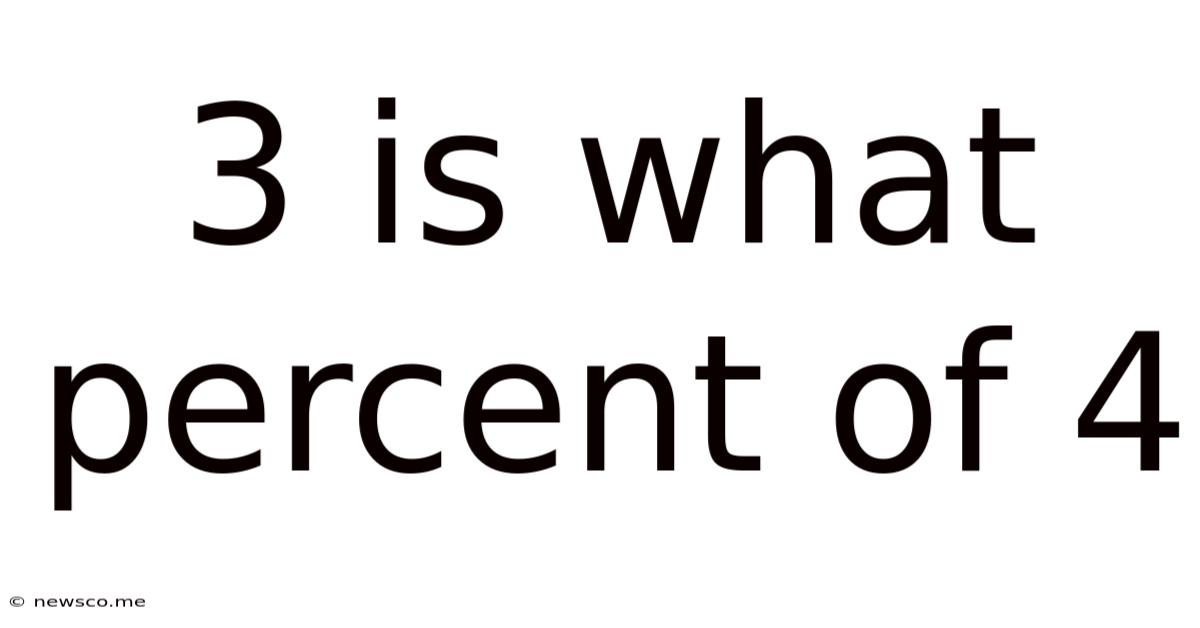
Table of Contents
3 is What Percent of 4? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in math with wide-ranging applications in everyday life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves deep into the question, "3 is what percent of 4?", providing a step-by-step solution, exploring different approaches, and highlighting practical applications of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are incredibly useful because they provide a standardized way to compare different quantities, even if those quantities are vastly different in size.
Calculating "3 is What Percent of 4?"
Let's tackle the core question: 3 is what percent of 4? There are several ways to solve this problem, each offering a slightly different perspective on the underlying concept.
Method 1: Using the Percentage Formula
The fundamental formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 3 (the number we're interested in expressing as a percentage)
- Whole: 4 (the total number)
Substituting these values into the formula, we get:
(3 / 4) x 100% = 0.75 x 100% = 75%
Therefore, 3 is 75% of 4.
Method 2: Setting up a Proportion
Another way to approach this is by setting up a proportion:
3/4 = x/100
Here, 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
4x = 300
x = 300 / 4
x = 75
Again, we arrive at the answer: 3 is 75% of 4.
Method 3: Using Decimal Conversion
We can also solve this by first converting the fraction 3/4 into a decimal:
3 ÷ 4 = 0.75
Then, multiply the decimal by 100% to express it as a percentage:
0.75 x 100% = 75%
This method emphasizes the relationship between decimals and percentages.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in various real-world scenarios. Here are some examples:
1. Sales and Discounts:
Imagine a store offers a 25% discount on a $40 item. To calculate the discount, you'd find 25% of $40: (0.25 x $40) = $10. The final price would be $40 - $10 = $30. Conversely, if you know the original price and the discounted price, you can calculate the percentage discount.
2. Taxes and Interest:
Calculating sales tax or interest on loans involves percentage calculations. For instance, a 6% sales tax on a $100 purchase would be (0.06 x $100) = $6. Similarly, calculating compound interest requires repeated percentage calculations over time.
3. Grade Calculation:
In education, percentages are used to represent grades. If you score 30 out of 40 on a test, your percentage score is (30/40) x 100% = 75%.
4. Data Analysis:
Percentages are critical in data analysis for expressing proportions and comparing different groups or categories. For example, if a survey shows 3 out of 4 people prefer a certain product, this can be expressed as 75% preference.
5. Financial Planning:
Budgeting, investment returns, and analyzing financial statements heavily rely on percentage calculations. Understanding percentage changes in income, expenses, or asset values is crucial for making informed financial decisions.
Beyond the Basics: Working with More Complex Percentages
While the example of "3 is what percent of 4" is relatively straightforward, percentage calculations can become more complex. Here are some scenarios to consider:
-
Finding the Whole: If you know the percentage and the part, you can calculate the whole. For example, if 25% of a number is 5, you can set up the equation: 0.25x = 5. Solving for x gives you the whole number (20).
-
Finding the Part: If you know the percentage and the whole, you can find the part. For instance, 15% of 60 is (0.15 x 60) = 9.
-
Percentage Increase/Decrease: Calculating percentage change involves finding the difference between two numbers and expressing it as a percentage of the original number. For example, if a value increases from 10 to 12, the percentage increase is [(12-10)/10] x 100% = 20%.
-
Compound Percentages: When percentages are applied repeatedly, it's called compounding. This is commonly seen in interest calculations where interest earned is added to the principal, and subsequent interest is calculated on the larger amount.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The key to mastering percentages is consistent practice. Work through various examples and problems to build your understanding and speed.
-
Use a Calculator: For more complex calculations, using a calculator can save time and ensure accuracy. Many calculators have a percentage function that simplifies the process.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying concepts of fractions, decimals, and proportions to tackle any percentage problem effectively.
-
Visual Aids: Visual aids such as charts and graphs can help understand and represent percentage data more intuitively.
Conclusion: The Importance of Percentage Literacy
The ability to accurately and efficiently calculate percentages is a valuable skill applicable across many areas of life. Understanding percentage calculations empowers you to make informed decisions in finance, shopping, education, and data analysis. By mastering these fundamental concepts and practicing regularly, you can confidently tackle any percentage-related challenge. The seemingly simple question, "3 is what percent of 4?", serves as a springboard to understanding a vast and crucial mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 Is What Percent Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.