3 Raised To The Power Of 4
News Co
Apr 16, 2025 · 5 min read
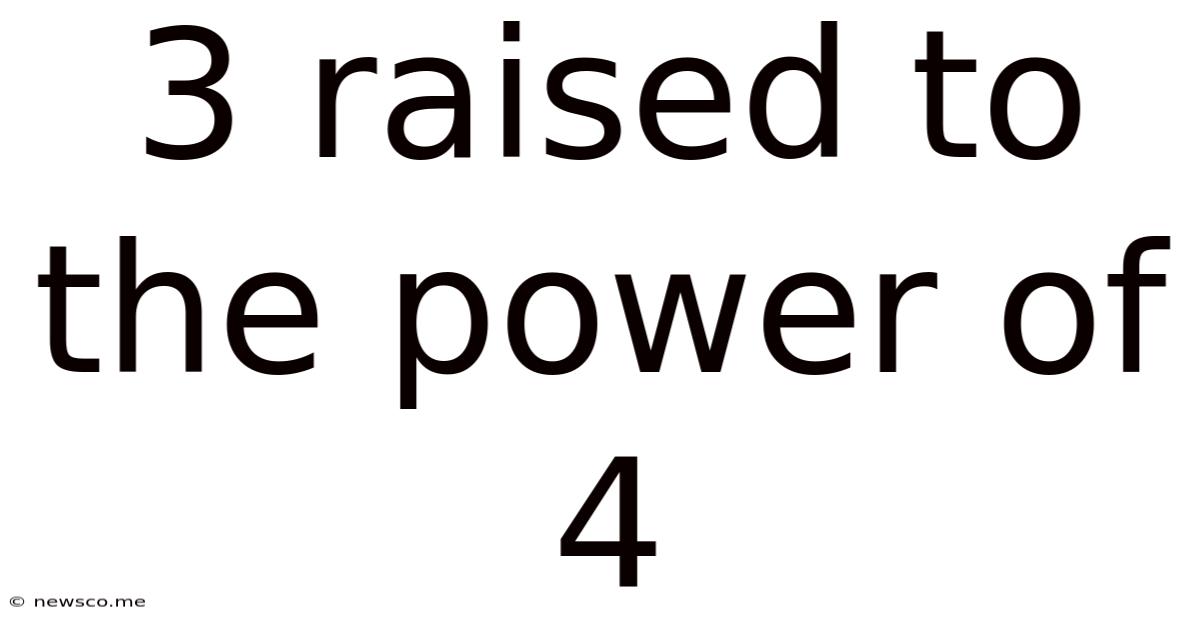
Table of Contents
3 Raised to the Power of 4: Unveiling the Math Behind the Number 81
The seemingly simple expression "3 raised to the power of 4," or 3<sup>4</sup>, holds a surprising depth when explored. While the answer, 81, might seem straightforward, delving into its mathematical implications reveals connections to various fields, from basic arithmetic to advanced concepts. This article will dissect this fundamental mathematical concept, exploring its calculation, applications, and broader significance in various mathematical contexts.
Understanding Exponents: A Foundation
Before diving into 3<sup>4</sup>, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. In the expression a<sup>n</sup>, 'a' represents the base, and 'n' represents the exponent. Therefore, 3<sup>4</sup> signifies that the base number 3 is multiplied by itself four times: 3 × 3 × 3 × 3.
Calculating 3 to the Power of 4
The calculation is straightforward:
- 3 × 3 = 9 (3 squared, or 3²)
- 9 × 3 = 27 (3 cubed, or 3³)
- 27 × 3 = 81 (3 to the power of 4, or 3<sup>4</sup>)
Therefore, 3 raised to the power of 4 equals 81. This seemingly simple calculation opens doors to a world of mathematical possibilities.
Applications of 3<sup>4</sup> = 81
The number 81, derived from 3<sup>4</sup>, appears in various mathematical and real-world scenarios. Its presence isn't always immediately obvious, but understanding its origins helps us appreciate its significance.
Geometry and Spatial Reasoning
-
Squares and Cubes: The number 81 is directly related to geometric shapes. Consider a square with sides of length 9 units. Its area would be 9 x 9 = 81 square units. Similarly, imagine a cube with sides of 3 units. If we consider 3 layers of 9 unit squares, the result is a volume of 27 cubic units (3³). In essence, 3<sup>4</sup> (81) relates to these geometric concepts. While not directly the volume of a cube, it represents an area within a larger geometric structure.
-
Fractal Geometry: Fractals, complex geometric shapes with self-similar patterns, frequently involve exponential calculations. Though 3<sup>4</sup> might not directly define a specific fractal, the exponential relationship itself is a fundamental building block in their mathematical description. The iterative nature of calculating exponents is akin to the repetitive self-similarity found in many fractals.
Number Theory and its Significance
-
Perfect Squares: 81 is a perfect square, meaning it's the square of an integer (9² = 81). This property connects it to other mathematical concepts like Pythagorean triples and quadratic equations.
-
Divisibility: Understanding the prime factorization of 81 (3<sup>4</sup>) provides insight into its divisibility. It's divisible by 1, 3, 9, 27, and 81. This knowledge is crucial in number theory and various applications such as cryptography.
-
Modular Arithmetic: In modular arithmetic, where numbers "wrap around" after reaching a certain modulus, 81 plays a role. Its properties, derived from its prime factorization, influence calculations within modular systems.
Real-World Applications
While less direct than the mathematical applications, 3<sup>4</sup> = 81 finds subtle real-world relevance:
-
Combinatorics: In scenarios involving combinations and permutations, exponential calculations often arise. Consider a situation with three options, each chosen four times. The total number of possibilities would involve powers of 3. While it might not always result in exactly 81 possibilities, the underlying principle is based on exponential growth.
-
Computer Science: Binary systems in computer science utilize powers of 2. However, the principles of exponentiation are foundational across various computer science domains, such as algorithms and data structures, where exponential growth or decay plays a vital role in computational complexity. Although 3<sup>4</sup> might not directly represent a specific computer-related function, the broader concept of exponentiation is essential.
Extending the Concept: Beyond 3<sup>4</sup>
The exploration of 3<sup>4</sup> provides a springboard to understanding more complex exponential concepts:
Negative Exponents
What happens when the exponent is negative? 3<sup>-4</sup> is equivalent to 1/3<sup>4</sup> = 1/81. Negative exponents represent reciprocals.
Fractional Exponents
Fractional exponents, like 3<sup>4/2</sup> (which simplifies to 3² = 9), introduce the concept of roots. The denominator represents the root (in this case, a square root), and the numerator is the power.
Exponential Growth and Decay
The concept of raising a number to a power is central to exponential growth and decay models. These models describe phenomena where quantities increase or decrease at a rate proportional to their current value. Understanding this concept is crucial in fields like finance (compound interest), biology (population growth), and physics (radioactive decay).
Connecting the Dots: Mathematical Interconnectedness
The seemingly simple equation 3<sup>4</sup> = 81 reveals a fascinating interconnectedness within mathematics. Its implications extend beyond simple arithmetic, encompassing geometry, number theory, and broader mathematical concepts. Understanding this interconnectedness is crucial for appreciating the elegance and power of mathematics as a whole.
Conclusion: The Significance of a Simple Equation
The seemingly mundane calculation of 3<sup>4</sup> = 81 serves as a microcosm of the vastness and interconnectedness of mathematics. From its geometric interpretations to its role in number theory and its subtle presence in real-world applications, this fundamental equation highlights the profound implications even of seemingly simple mathematical concepts. A deeper understanding of exponentiation, starting with this seemingly basic example, opens doors to a richer appreciation of mathematics' power and its pervasive influence on our world. Its significance reaches far beyond the simple number 81 itself, demonstrating the foundational role of such calculations in more complex mathematical structures and applications. By exploring the intricacies of this simple equation, we uncover layers of mathematical depth and beauty, furthering our understanding of the underlying principles that govern numerical relationships and their manifestation in various aspects of our lives.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 Raised To The Power Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.