3 To The 3rd Power Equals
News Co
Apr 25, 2025 · 5 min read
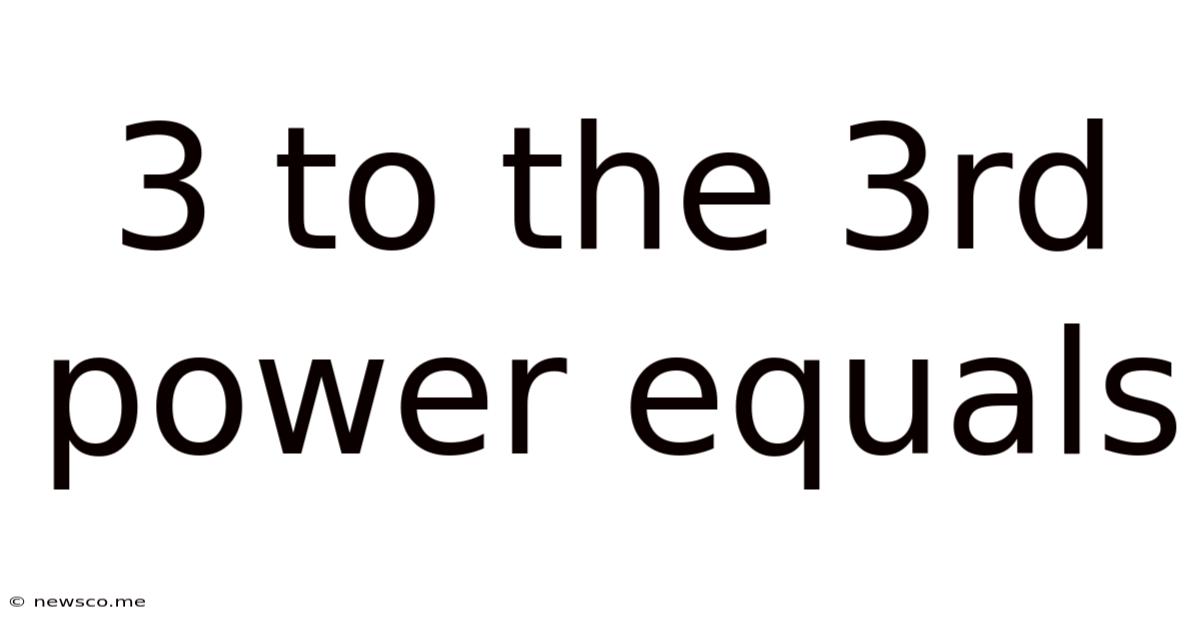
Table of Contents
3 to the 3rd Power Equals: Unveiling the Fundamentals of Exponentiation
The seemingly simple question, "3 to the 3rd power equals what?", opens a door to a vast world of mathematical concepts, from fundamental arithmetic to advanced calculus. This comprehensive guide will not only answer that question but will also delve into the underlying principles of exponentiation, exploring its applications and significance in various fields.
Understanding Exponentiation: Beyond Simple Multiplication
Exponentiation, at its core, is repeated multiplication. It's a shorthand way of expressing a number multiplied by itself a certain number of times. The expression "3 to the 3rd power," or 3³, is a concise representation of 3 multiplied by itself three times: 3 x 3 x 3.
Key Components of Exponentiation:
- Base: The number being multiplied (in this case, 3).
- Exponent: The number indicating how many times the base is multiplied by itself (in this case, 3).
- Power: The result of the exponentiation (which we'll solve shortly).
Calculating 3 to the 3rd Power (3³)
The calculation is straightforward:
3 x 3 x 3 = 27
Therefore, 3 to the 3rd power equals 27.
Expanding the Concept: Exploring Different Exponents
While we've focused on 3³, understanding exponentiation requires exploring various exponent values. Let's examine a few scenarios:
1. Exponent of 1:
Any number raised to the power of 1 equals itself. For example, 3¹ = 3. This is because the base is only multiplied by itself once.
2. Exponent of 0:
Any non-zero number raised to the power of 0 equals 1. For example, 3⁰ = 1. This might seem counterintuitive, but it's a fundamental rule in mathematics, stemming from the properties of exponents and maintaining consistency in mathematical operations.
3. Exponent of 2 (Squaring):
Raising a number to the power of 2 is known as squaring. For example, 3² = 3 x 3 = 9. This represents the area of a square with sides of length 3.
4. Negative Exponents:
A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example:
3⁻¹ = 1/3¹ = 1/3 3⁻² = 1/3² = 1/9
5. Fractional Exponents:
Fractional exponents represent roots. For example:
3^(1/2) = √3 (the square root of 3) 3^(1/3) = ³√3 (the cube root of 3)
Applications of Exponentiation: Real-World Examples
Exponentiation is not just an abstract mathematical concept; it finds widespread applications in various fields:
1. Science:
-
Exponential Growth/Decay: Many natural phenomena, such as population growth, radioactive decay, and compound interest, exhibit exponential behavior. These are modeled using exponential functions, which rely heavily on exponentiation.
-
Physics: Exponentiation plays a crucial role in describing various physical processes, including calculating energy levels in quantum mechanics and describing the intensity of electromagnetic radiation.
2. Finance:
- Compound Interest: The power of compound interest, where interest is earned not only on the principal but also on accumulated interest, is a direct application of exponentiation. The formula for compound interest involves raising a number (1 + interest rate) to the power of the number of compounding periods.
3. Computer Science:
-
Big O Notation: In computer science, big O notation is used to describe the efficiency of algorithms. Exponential time complexity, denoted as O(2ⁿ) or O(kⁿ), indicates that the runtime of an algorithm grows exponentially with the input size, which can lead to significant performance issues for large datasets.
-
Binary Numbers: The binary number system, fundamental to computer architecture, uses powers of 2 to represent numbers. For example, the binary number 1011 represents 1 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2⁰ = 11 in decimal.
Beyond the Basics: Exploring More Advanced Concepts
While we've covered the fundamental aspects, exponentiation extends far beyond simple calculations. Let's briefly touch upon more advanced concepts:
1. Logarithms:
Logarithms are the inverse of exponentiation. If 3³ = 27, then the logarithm base 3 of 27 is 3 (log₃27 = 3). Logarithms are used to solve equations involving exponents and find the exponent when the base and the result are known.
2. Complex Numbers:
Exponentiation can also be applied to complex numbers, which involve the imaginary unit 'i' (√-1). This leads to fascinating results and applications in areas like electrical engineering and signal processing.
Mastering Exponentiation: Tips and Practice
Developing a strong understanding of exponentiation requires consistent practice and a firm grasp of fundamental mathematical principles. Here are some helpful tips:
-
Start with the basics: Make sure you understand the concept of repeated multiplication before tackling more complex problems.
-
Practice regularly: Solve a variety of problems with different bases and exponents, including negative and fractional exponents.
-
Use online resources: Many websites and educational platforms offer interactive exercises and tutorials on exponentiation.
-
Break down complex problems: When confronted with a challenging problem, break it down into smaller, manageable steps.
-
Understand the properties of exponents: Familiarize yourself with the rules of exponents, such as the product rule, quotient rule, and power rule, to simplify complex expressions.
Conclusion: The Enduring Significance of Exponentiation
From simple arithmetic calculations to complex scientific models, exponentiation plays a fundamental role in our understanding of the world. The seemingly simple question "3 to the 3rd power equals what?" serves as a gateway to exploring a vast and influential mathematical concept with far-reaching applications across various disciplines. By mastering the fundamentals and exploring its advanced applications, you'll unlock a deeper understanding of mathematical principles and their significance in the real world. So, remember: 3³ = 27, but the implications extend far beyond this single numerical answer.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 To The 3rd Power Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.