3 To The Second Power Equals
News Co
Apr 17, 2025 · 5 min read
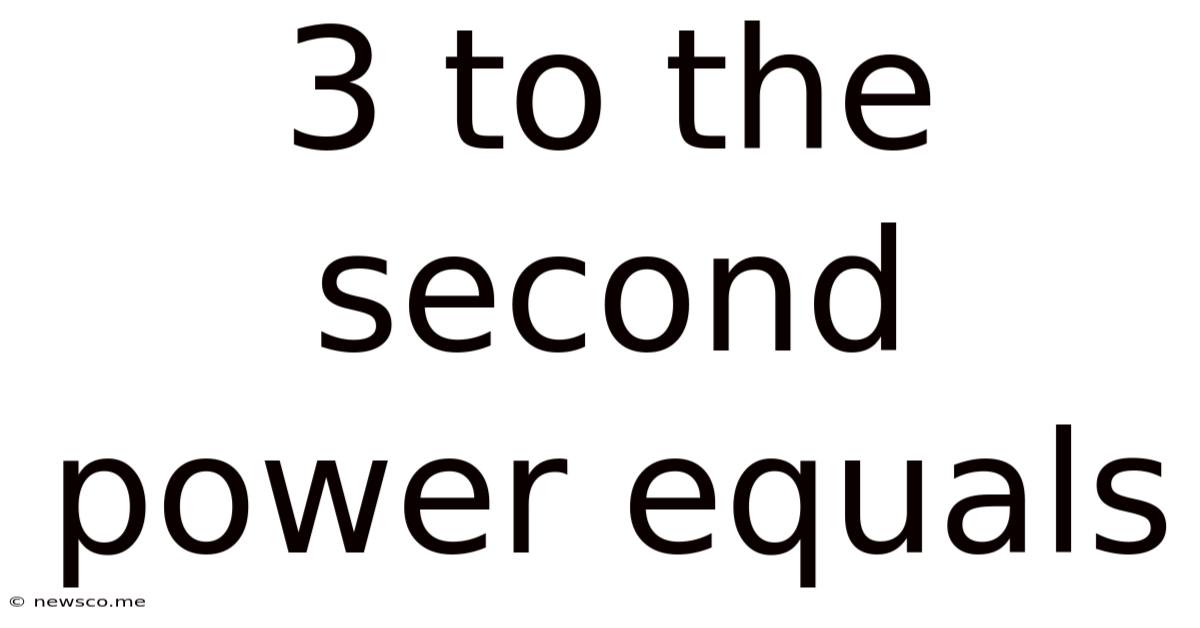
Table of Contents
3 to the Second Power Equals: Unveiling the Fundamentals of Exponents
The seemingly simple statement, "3 to the second power equals," opens a door to a vast and fascinating world of mathematics. Understanding this fundamental concept, and its broader implications within exponents and powers, is crucial for anyone seeking a solid grasp of mathematical principles. This comprehensive guide will delve into the meaning of "3 to the second power," exploring its calculation, applications, and the wider context of exponential notation. We'll unravel the mystery behind exponents, demonstrate their practical uses, and even touch upon their advanced applications.
Understanding Exponents and Powers
Before diving into the specific calculation of 3 to the second power, let's establish a clear understanding of exponents and powers. In mathematics, an exponent (also called a power or index) is a number that indicates how many times a base number is multiplied by itself. The base number is the number being multiplied repeatedly. The entire expression is called a power.
For instance, in the expression 3², 3 is the base and 2 is the exponent. This expression is read as "3 to the power of 2" or "3 squared." It signifies that the base number, 3, is multiplied by itself twice: 3 x 3.
Calculating 3 to the Second Power
Now, let's address the question directly: What does 3 to the second power equal? As we've established, 3² means 3 multiplied by itself twice:
3² = 3 x 3 = 9
Therefore, 3 to the second power equals 9. This seemingly simple calculation forms the foundation for many more complex mathematical operations.
Expanding the Concept: Beyond 3²
While understanding 3² is essential, it's vital to grasp the broader implications of exponents. Let's explore some related concepts:
Different Exponents, Same Base:
- 3¹ (3 to the power of 1): Any number raised to the power of 1 equals itself. Therefore, 3¹ = 3.
- 3³ (3 to the power of 3 or 3 cubed): This means 3 x 3 x 3 = 27.
- 3⁴ (3 to the power of 4): This means 3 x 3 x 3 x 3 = 81.
- 3⁰ (3 to the power of 0): Any non-zero number raised to the power of 0 equals 1. Therefore, 3⁰ = 1. This might seem counterintuitive at first, but it's a fundamental rule in exponential mathematics.
- 3⁻¹ (3 to the power of -1): Negative exponents represent reciprocals. 3⁻¹ = 1/3.
- 3⁻² (3 to the power of -2): This means 1/(3²) = 1/9.
These examples illustrate how the value of a power changes drastically with different exponents, even when the base remains constant.
Different Bases, Same Exponent:
Let's now explore the effect of changing the base while keeping the exponent constant at 2 (squared):
- 2² = 2 x 2 = 4
- 4² = 4 x 4 = 16
- 5² = 5 x 5 = 25
- 10² = 10 x 10 = 100
This demonstrates that even a small change in the base significantly impacts the final result when the exponent is greater than 1.
Practical Applications of Exponents
Exponents are far from being a purely theoretical concept; they have numerous real-world applications across various fields:
Science and Engineering:
- Exponential Growth and Decay: Exponents are crucial for modeling exponential growth (e.g., population growth, compound interest) and decay (e.g., radioactive decay, drug metabolism). The formula for compound interest, for example, heavily relies on exponential functions.
- Physics: Exponents are essential in physics for describing various phenomena, including the inverse square law (e.g., gravitational force, light intensity).
- Chemistry: Chemical reactions often involve exponential relationships between reactants and products.
Finance and Economics:
- Compound Interest: As mentioned earlier, compound interest calculations directly use exponents to determine the future value of an investment.
- Inflation: Understanding exponential growth is critical for analyzing inflation and its impact on the economy.
Computer Science:
- Big O Notation: Exponents are used extensively in computer science to describe the efficiency of algorithms using Big O notation. This notation helps programmers understand how the runtime or space requirements of an algorithm scale with the input size.
Everyday Life:
While less obvious, exponents also appear in everyday situations:
- Area Calculations: The area of a square is calculated by squaring the length of its side (side²).
- Volume Calculations: The volume of a cube is calculated by cubing the length of its side (side³).
Advanced Concepts Related to Exponents
Beyond the basic calculations, several advanced concepts build upon the foundation of exponents:
Scientific Notation:
Scientific notation uses exponents to represent very large or very small numbers concisely. For example, the speed of light is approximately 3 x 10⁸ meters per second.
Logarithms:
Logarithms are the inverse functions of exponents. They provide a way to solve for the exponent when the base and the result are known. For example, the logarithm base 3 of 9 (log₃9) is 2 because 3² = 9.
Fractional and Decimal Exponents:
Exponents aren't limited to whole numbers. Fractional exponents represent roots, and decimal exponents can represent more precise values. For example:
- 3¹/² = √3 (the square root of 3)
- 3¹.⁵ ≈ 5.196
Complex Numbers and Exponents:
Exponents can also be applied to complex numbers, leading to interesting and useful results in advanced mathematics and physics.
Conclusion: The Significance of "3 to the Second Power Equals 9"
The seemingly simple equation, "3 to the second power equals 9," serves as a gateway to a much larger world of mathematical concepts and applications. Understanding exponents and their properties is crucial not only for academic success but also for navigating many aspects of the real world, from finance and science to computer science and engineering. By grasping the fundamentals, we unlock the power of exponential notation and its far-reaching influence. The ability to solve and interpret exponential expressions is a valuable skill that transcends the confines of the classroom and empowers us to analyze and understand complex phenomena in diverse fields. Remember, the journey begins with a solid understanding of the basics, and the simple calculation 3² = 9 is an excellent starting point.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 To The Second Power Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.