3 To The Third Power Equals
News Co
Apr 22, 2025 · 5 min read
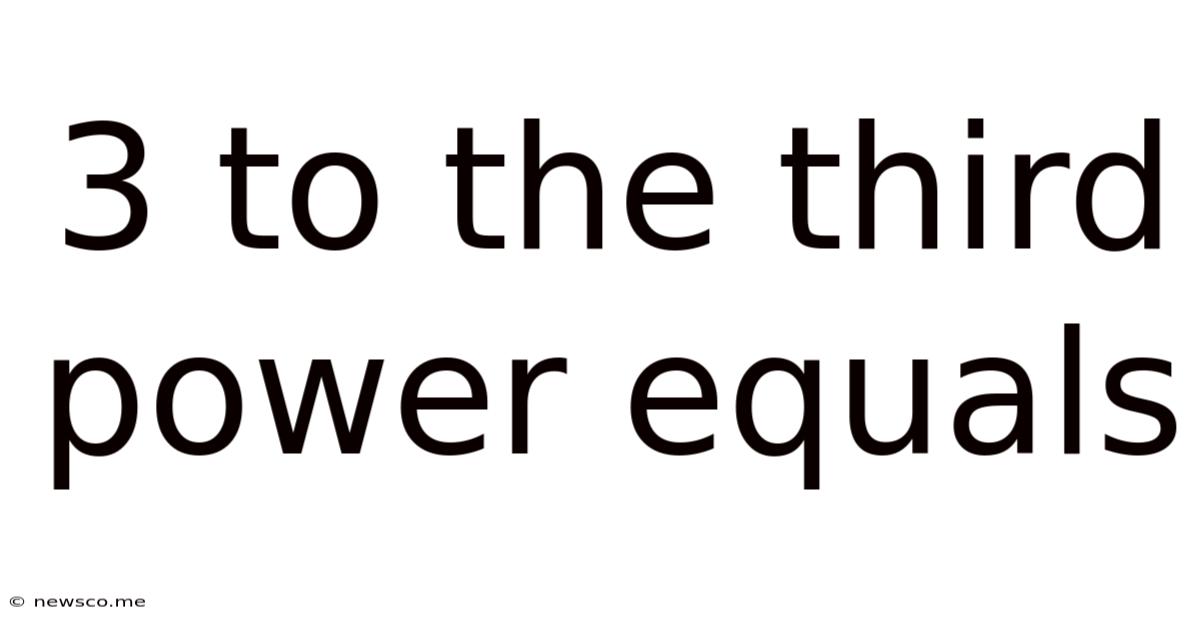
Table of Contents
3 to the Third Power Equals: Unveiling the Wonders of Exponentiation
The seemingly simple equation, "3 to the third power equals," holds within it the key to understanding a fundamental concept in mathematics: exponentiation. While the answer – 27 – is readily available through a quick calculation, delving deeper reveals the rich tapestry of applications and implications this seemingly basic concept possesses. This article explores the meaning of 3 to the third power, its mathematical underpinnings, diverse applications across various fields, and its significance in expanding our understanding of numerical relationships.
Understanding Exponentiation: Beyond Simple Multiplication
At its core, exponentiation represents repeated multiplication. The expression "3 to the third power," or 3³, signifies 3 multiplied by itself three times: 3 x 3 x 3. The base number (3 in this case) is the number being multiplied, and the exponent (3) indicates how many times the base is multiplied by itself. This process contrasts with simple multiplication, which involves multiplying two distinct numbers. Exponentiation introduces a new level of mathematical complexity, leading to rapid growth as the exponent increases.
The Power of Notation: Understanding Exponents
Mathematical notation plays a crucial role in simplifying complex expressions. The superscript notation (³) is incredibly efficient, providing a concise way to represent repeated multiplication. Imagine writing out 3 x 3 x 3 x 3 x 3 x 3 x 3… for larger exponents; the notation becomes increasingly unwieldy. Exponents provide elegance and clarity, streamlining mathematical operations and enhancing understanding.
Calculating 3 to the Third Power: A Step-by-Step Approach
Calculating 3³ is straightforward, but understanding the process is fundamental. Here’s a breakdown:
- Identify the Base and Exponent: In the expression 3³, the base is 3, and the exponent is 3.
- Perform the Repeated Multiplication: Multiply the base by itself the number of times specified by the exponent. This means 3 x 3 x 3.
- Calculate the Result: 3 x 3 = 9. Then, 9 x 3 = 27. Therefore, 3³ = 27.
This seemingly simple calculation forms the foundation for more complex mathematical operations and concepts.
Expanding the Horizons: Applications of Exponentiation
The concept of exponentiation, exemplified by 3³, extends far beyond basic arithmetic. Its applications permeate various fields, including:
1. Science and Engineering: Exponential Growth and Decay
Exponential functions, based on the principle of exponentiation, are crucial in modeling various phenomena in science and engineering. Examples include:
- Population Growth: The growth of bacterial colonies, animal populations, or even human populations often follows an exponential pattern. Understanding exponential growth is essential in predicting future population sizes and managing resources.
- Radioactive Decay: The decay of radioactive materials follows an exponential decay curve. This principle is essential in carbon dating and nuclear engineering.
- Compound Interest: The growth of money in a savings account, when interest is compounded, follows an exponential function. Understanding compound interest is vital for financial planning and investment strategies.
2. Computer Science: Data Structures and Algorithms
Exponentiation plays a significant role in computer science:
- Big O Notation: This notation is used to describe the efficiency of algorithms. Many algorithms exhibit exponential time complexity, meaning their runtime increases exponentially with the input size. Understanding exponential complexity is critical for optimizing software performance.
- Binary Representation: Computers operate using binary code (0s and 1s). Exponentiation is inherent in converting between binary and decimal representations.
- Hashing Algorithms: These algorithms use exponentiation for generating unique identifiers for data elements, which are vital in database management and information retrieval.
3. Geometry and Measurement: Volume Calculations
Exponentiation finds application in geometric calculations:
- Volume of a Cube: The volume of a cube with side length 's' is calculated as s³. Therefore, a cube with a side length of 3 units has a volume of 3³ = 27 cubic units.
- Volume of other 3D shapes: Similar calculations involving exponents are used to find the volumes of other three-dimensional shapes.
4. Finance and Economics: Compound Interest and Inflation
In finance, exponentiation models the power of compounding:
- Compound Interest: As mentioned earlier, the growth of an investment with compound interest follows an exponential growth pattern. The formula for compound interest involves exponentiation directly.
- Inflation: The cumulative effect of inflation over time is also often modeled using exponential functions. Understanding exponential growth in this context helps in planning for long-term financial goals.
Beyond 3³: Exploring Higher Powers and Other Bases
While this article focuses on 3³, the concepts discussed extend to other bases and higher powers. Understanding the general principle of exponentiation allows for calculations involving any base and exponent. For example:
- 2⁵ (2 to the fifth power): 2 x 2 x 2 x 2 x 2 = 32
- 5² (5 squared): 5 x 5 = 25
- 10⁴ (10 to the fourth power): 10 x 10 x 10 x 10 = 10,000
The ability to manipulate and understand exponential expressions is critical for solving a wide range of mathematical problems.
Expanding Mathematical Understanding: The Significance of Exponentiation
The seemingly simple equation, 3³ = 27, serves as a gateway to a vast and intricate world of mathematical concepts. Understanding exponentiation unlocks the ability to model complex phenomena, optimize algorithms, and perform intricate calculations across numerous disciplines. Mastering this fundamental concept provides a solid foundation for further exploration in algebra, calculus, and numerous other advanced mathematical fields.
Conclusion: From Simple Calculation to Powerful Applications
The journey from a simple calculation like "3 to the third power equals 27" to understanding the broader implications of exponentiation highlights the power and beauty of mathematics. This seemingly basic equation opens doors to a wide array of applications, underscoring the importance of mastering fundamental mathematical concepts. As we continue to explore the world around us, a strong grasp of exponentiation will prove invaluable in understanding the intricate relationships that govern our universe. From the growth of populations to the decay of radioactive materials and the intricacies of financial markets, the concept of 3 cubed, and indeed exponentiation in general, provides a framework for comprehension and prediction across a vast spectrum of fields. The elegance and efficiency of mathematical notation, combined with the power of the underlying concepts, empowers us to solve complex problems and unlock deeper insights into the world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 To The Third Power Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.