3 X 2 2 2x 3
News Co
Apr 20, 2025 · 5 min read
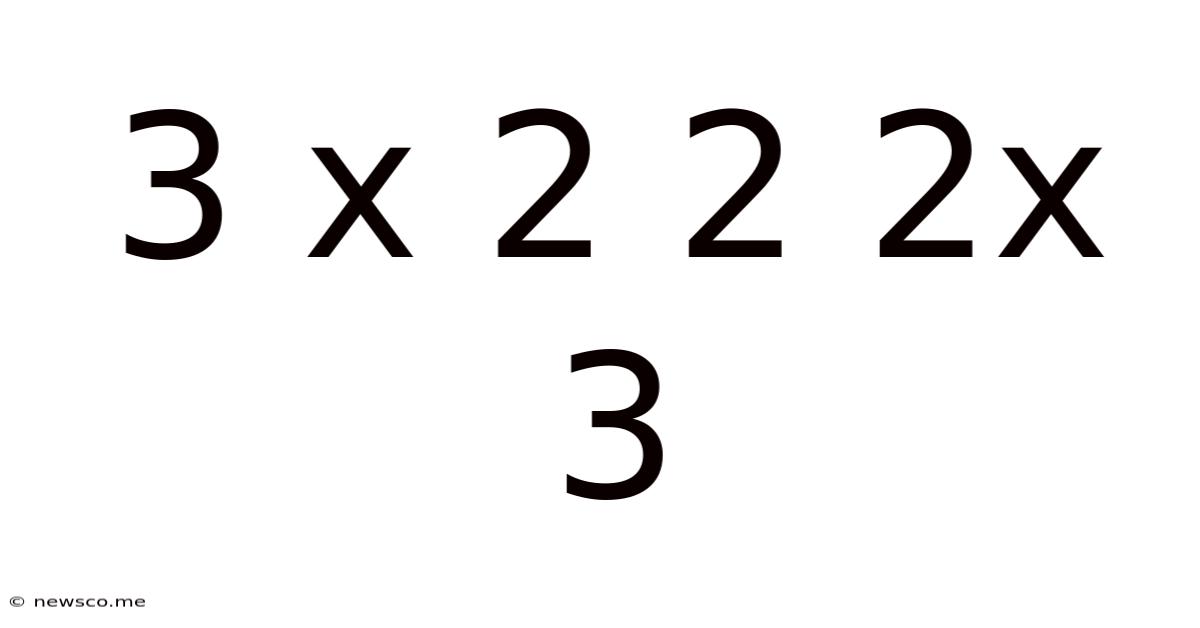
Table of Contents
Decoding the Enigma: A Deep Dive into 3 x 2 2 2 x 3
The seemingly simple expression "3 x 2 2 2 x 3" presents a fascinating puzzle, especially when considering the ambiguity inherent in its lack of explicit operational precedence. This seemingly straightforward mathematical statement opens a door to exploring order of operations, different interpretations, and the importance of clear communication in mathematics. This article will delve into the various interpretations, solutions, and the broader implications of this ambiguous expression.
Understanding Order of Operations (PEMDAS/BODMAS)
Before tackling the various interpretations of "3 x 2 2 2 x 3", it's crucial to understand the fundamental principles of order of operations. This set of rules dictates the sequence in which mathematical operations should be performed to obtain a consistent and unambiguous result. These rules are often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same order of operations.
The Importance of Clarity and Parentheses
The core issue with "3 x 2 2 2 x 3" lies in the absence of parentheses or other explicit indicators of operational precedence. Without them, different interpretations are possible, leading to different results. Parentheses are crucial tools in mathematics for grouping operations and ensuring clarity. They provide a clear indication of which calculations should be prioritized.
Interpretation 1: Strict Left-to-Right Evaluation
One possible interpretation is to evaluate the expression strictly from left to right, without any inherent precedence between multiplication operations. This approach would yield the following calculation:
3 x 2 = 6
6 x 2 = 12
12 x 2 = 24
24 x 3 = 72
Therefore, under this strict left-to-right interpretation, the solution to "3 x 2 2 2 x 3" is 72.
Strengths and Weaknesses of Left-to-Right Evaluation
The strength of this approach lies in its simplicity and straightforward application. It eliminates the need for any subjective interpretation of precedence. However, its weakness is that it contradicts the standard order of operations, which generally prioritizes multiplication and division over addition and subtraction. This approach might lead to confusion and inconsistencies in more complex expressions.
Interpretation 2: Implicit Grouping (Multiplication Grouping)
Another interpretation could be to treat consecutive numbers as implicitly grouped multiplication operations. This assumes that the expression should be understood as:
(3 x 2) x (2 x 2) x 3
This would lead to the following calculation:
(3 x 2) = 6
(2 x 2) = 4
6 x 4 = 24
24 x 3 = 72
This interpretation, while potentially more intuitive for some, still results in the same solution of 72. However, it highlights the implicit grouping and the need for clear notation to avoid potential misinterpretations.
Interpretation 3: The Role of Concatenation (A Non-Mathematical Interpretation)
In certain programming languages or contexts where concatenation (joining strings of characters) is involved, the expression might be interpreted entirely differently. In such scenarios, the numbers could be treated as strings to be concatenated, resulting in the string "32223". This is, however, entirely outside the realm of standard mathematical interpretation and highlights the importance of specifying the context.
Beyond the Numbers: Implications in Programming and Computer Science
The ambiguity in "3 x 2 2 2 x 3" underscores a critical concept in programming: the importance of explicit operator precedence. Programming languages utilize operator precedence rules similar to PEMDAS/BODMAS, but these rules must be clearly defined to avoid unexpected results. Failure to specify precedence through parentheses or other unambiguous notation can lead to bugs and errors in software.
The Crucial Role of Notation in Mathematics and Beyond
The ambiguity of "3 x 2 2 2 x 3" emphasizes the critical role of clear and unambiguous notation in mathematics, programming, and even everyday communication. In mathematics, proper use of parentheses, brackets, and other symbols is not just a stylistic choice; it's essential for ensuring that the intended operations are executed correctly. Ambiguous notation can lead to errors, confusion, and inconsistent results.
Improving Clarity: Practical Applications and Examples
To avoid the ambiguity presented by "3 x 2 2 2 x 3", the expression should always be rewritten with explicit multiplication symbols and parentheses to clarify the intended order of operations. For instance:
- (3 x 2) x (2 x 2) x 3 = 72 (Clear grouping)
- 3 x (2 x 2 x 2) x 3 = 72 (Grouping around the repeated 2s)
- 3 x 2 x 2 x 2 x 3 = 72 (All multiplications are equally weighted)
By explicitly using parentheses or consistently employing the left-to-right rule (in contexts where this is explicitly understood), we can remove any doubt about the intended calculation and ensure consistent results.
Extending the Concept: More Complex Expressions
The lessons learned from analyzing "3 x 2 2 2 x 3" can be extended to more complex mathematical expressions involving different operations and a greater number of operands. The consistent application of order of operations, along with the strategic use of parentheses, is crucial to avoid errors and ensure clarity.
For instance, consider the following expression:
3 + 2 x 4 – 6 ÷ 2
Following the order of operations (PEMDAS/BODMAS):
- Multiplication and Division (from left to right): 2 x 4 = 8 and 6 ÷ 2 = 3
- Addition and Subtraction (from left to right): 3 + 8 = 11 and 11 – 3 = 8
Therefore, the solution is 8. Again, clear notation is key to preventing misinterpretations.
Conclusion: The Power of Precision in Mathematics
The simple expression "3 x 2 2 2 x 3" might seem trivial at first glance, but it serves as a powerful reminder of the importance of clear and unambiguous notation in mathematics. The absence of explicit operational precedence can lead to multiple interpretations and inconsistent results. This highlights the necessity of employing parentheses or other clarifying symbols to ensure that calculations are performed correctly and that communication is precise and unambiguous. The lessons learned from analyzing this seemingly simple expression extend far beyond basic arithmetic, influencing the way we approach more complex mathematical problems and write code in computer programming. The power of precision in mathematics and related fields cannot be overstated. It underpins the accuracy and reliability of calculations, ensuring consistency and avoiding potential errors in diverse applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 X 2 2 2x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.