30 Is 25 Of What Number
News Co
Apr 13, 2025 · 5 min read
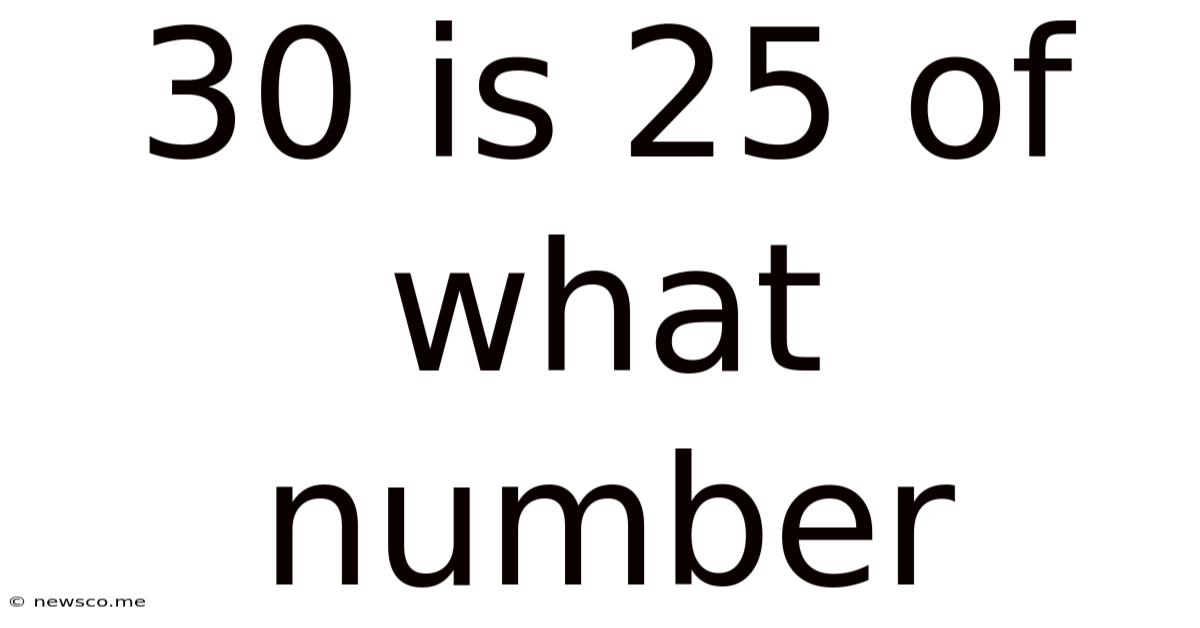
Table of Contents
30 is 25% of What Number? Solving Percentage Problems and Beyond
This seemingly simple question, "30 is 25% of what number?", opens a door to a world of practical applications of percentage calculations. Understanding how to solve this type of problem is crucial in various aspects of life, from calculating discounts and taxes to understanding financial statements and interpreting statistical data. This article will not only show you how to solve this specific problem but also delve into the underlying concepts, providing you with the tools to tackle any percentage calculation confidently.
Understanding Percentages: The Basics
Before jumping into the solution, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred." For instance, 25% means 25 out of 100, or 25/100, which simplifies to 1/4.
This fundamental understanding forms the basis for all percentage calculations. We often encounter percentages in everyday scenarios:
- Discounts: A 20% discount on a $100 item means you save $20 (20% of $100).
- Taxes: A 7% sales tax on a purchase means you'll pay an additional 7% of the purchase price.
- Interest Rates: Interest rates on loans and investments are expressed as percentages.
- Statistics: Data is frequently represented using percentages to illustrate proportions and trends.
Solving "30 is 25% of What Number?" – Method 1: Using the Formula
The most straightforward approach to solving this type of problem is using the percentage formula:
Part = Percentage × Whole
In our problem:
- Part: 30 (This is the value representing the 25%)
- Percentage: 25% (or 0.25 as a decimal – remember to convert percentages to decimals for calculations)
- Whole: This is what we need to find (let's represent it with 'x')
Substituting these values into the formula, we get:
30 = 0.25 × x
To solve for 'x', we divide both sides of the equation by 0.25:
x = 30 / 0.25
x = 120
Therefore, 30 is 25% of 120.
Solving "30 is 25% of What Number?" – Method 2: Using Proportions
Another effective method is setting up a proportion. Proportions involve two equivalent ratios. In this case, we can set up the proportion:
25/100 = 30/x
This proportion states that 25 parts out of 100 are equivalent to 30 parts out of the unknown whole (x).
To solve this proportion, we cross-multiply:
25x = 3000
Then, divide both sides by 25:
x = 3000 / 25
x = 120
Again, we arrive at the solution: 30 is 25% of 120.
Practical Applications and Real-World Examples
Understanding percentage calculations is invaluable in various real-world scenarios. Let's explore some examples:
-
Calculating Sales Tax: If you buy an item for $85 and the sales tax is 6%, you can calculate the tax amount: 0.06 × $85 = $5.10. The total cost would be $85 + $5.10 = $90.10.
-
Determining Discounts: A store offers a 15% discount on a $200 item. The discount amount is 0.15 × $200 = $30. The final price would be $200 - $30 = $170.
-
Analyzing Financial Statements: Companies use percentages to represent key financial metrics like profit margins, return on investment (ROI), and debt-to-equity ratios. Understanding these percentages is crucial for assessing a company's financial health.
-
Interpreting Survey Results: Surveys often present data using percentages. For example, a survey might indicate that 70% of respondents prefer a particular product. This percentage helps in understanding consumer preferences and making informed business decisions.
-
Calculating Tips: If you want to leave a 20% tip on a $50 meal, you would calculate 0.20 × $50 = $10.
-
Understanding Interest Rates: A loan with a 5% interest rate means you'll pay 5% of the principal amount as interest each year. Understanding this calculation is essential for managing personal finances.
Advanced Percentage Problems and Solutions
While the initial problem was relatively straightforward, let's explore more complex percentage scenarios:
Scenario 1: Finding the Percentage Increase or Decrease
Let's say a product's price increased from $50 to $60. To find the percentage increase:
- Calculate the difference: $60 - $50 = $10
- Divide the difference by the original price: $10 / $50 = 0.2
- Multiply by 100 to express as a percentage: 0.2 × 100 = 20%
Therefore, the price increased by 20%. Conversely, you can apply the same logic to calculate percentage decreases.
Scenario 2: Calculating the Original Price After a Percentage Discount
Suppose an item is sold for $75 after a 20% discount. To find the original price:
- Let 'x' represent the original price.
- Set up the equation: x - 0.20x = $75 (This represents the original price minus the 20% discount)
- Simplify: 0.80x = $75
- Solve for x: x = $75 / 0.80 = $93.75
Thus, the original price was $93.75.
Mastering Percentage Calculations: Tips and Tricks
-
Convert Percentages to Decimals: Always convert percentages to decimals (by dividing by 100) before performing calculations.
-
Use the Formula Consistently: The "Part = Percentage × Whole" formula is versatile and applicable to various percentage problems.
-
Practice Regularly: The more you practice solving percentage problems, the more confident and proficient you'll become.
-
Check Your Work: Always double-check your calculations to ensure accuracy.
-
Use Calculators Wisely: Calculators can help with complex calculations, but understanding the underlying principles remains essential.
Conclusion: The Power of Percentage Understanding
The seemingly simple question, "30 is 25% of what number?", has unveiled the practical importance of understanding percentage calculations. From everyday shopping to complex financial analysis, the ability to solve percentage problems is a valuable skill. By mastering the techniques and practicing regularly, you'll develop the confidence to tackle any percentage-related challenge, empowering you to make informed decisions in various aspects of your life. Remember to utilize the formula, practice consistently, and always check your work. With dedication, you can master this fundamental mathematical concept and unlock its significant practical applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about 30 Is 25 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.